I would be grateful for views about these thoughts!
It is important when teaching a topic to begin with a concept with which the student is already familiar. This helps the student to integrate the new information into what is known and to ‘understand’ it. For example, a medical student is told that 100 patients had been in a double-blind’ cross over randomised controlled trial and that 58 out of those 100 individuals had a BP higher on control than on treatment. Knowing only that a patient was one of those in the study, the probability of that patient having a BP difference greater than zero would be about 58/100 = 0.58. This shows a probability of 0.58 being estimated directly from the experience of 58/100 without involving Bayes rule (analogous to the approach of logistic regression). It would be the familiar way that anyone would form mental probabilities from the cumulative experience of being right or wrong about a series of predictions.
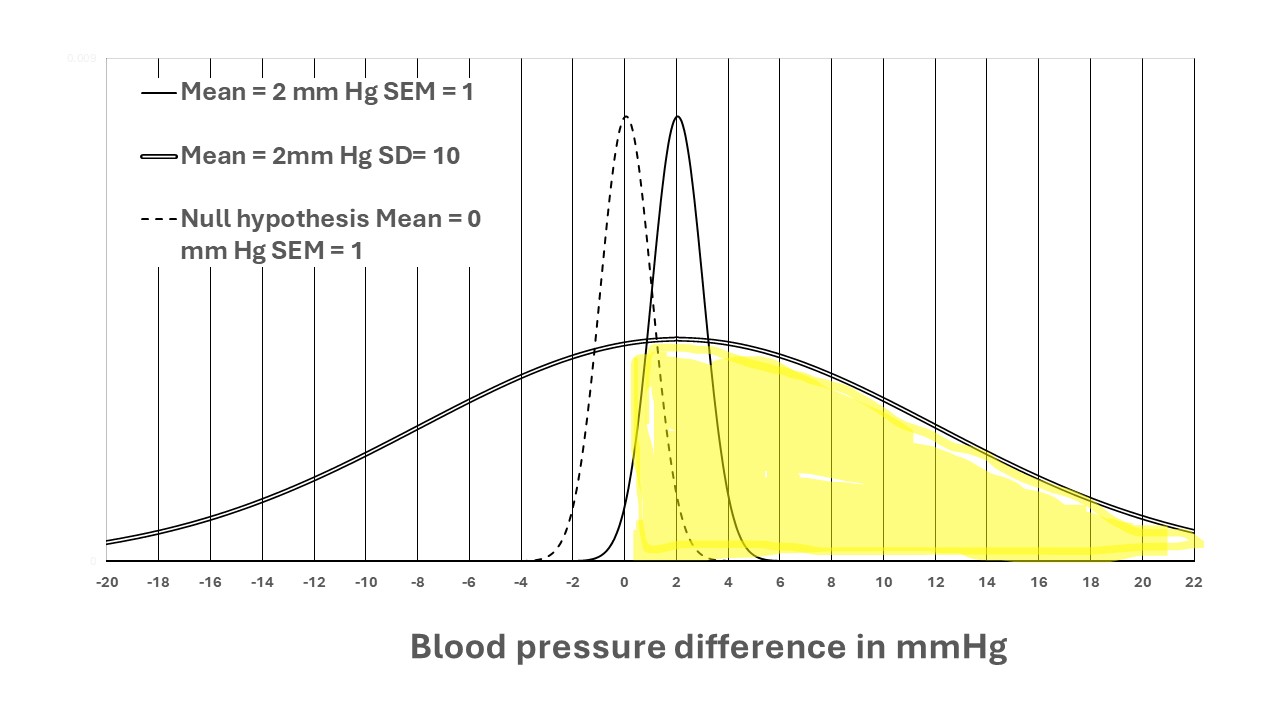
Figure 1: The distributions of blood pressure differences in a cross-over RCT
If the average BP difference between a pair of observations treatment and control was 2mmHg and the standard deviation of the differences was 10 mm Hg, then the shaded area under the bell-shaped Gaussian distribution above 0 mmHg (i.e. 0.2 standard deviations below the mean of 2mmHg (shaded yellow above) would contain 58% of the total area. As the standard deviation of the distribution was 10mm Hg and the number of observations was 100, then the standard error of all the possible means would be 10/√100 = 1 and the 95% of the area under the tall narrow curve with a mean of 2mm Hg and SEM of 1mmHg would fall between 2 mmHg +/- 1.96 = 0.04mm Hg to 3.96mm Hg. Zero would therefore be just outside these limits. If the study were repeated very many times and the mean found each time, the proportion and probability of a mean being higher than zero would be 0.9772, and the probability being zero or lower would be 0.0228. Again, this probability is derived from a direct probability of an outcome conditional on an observation without using Bayes rule. (This represents distribution 1 in post no 11).
We now assume a ‘null hypothesis’ that the true difference between the average BPs on treatment and control was zero (i.e. ‘true’ if we had made an infinite number of observations). We assume that 100 selections were made at random from this true population of zero difference. We also assume that the distribution of the differences is the same as in the above study (i.e. the bell-shaped Gaussian distribution) has a standard deviation of 10mm Hg and a standard error of the mean of 1mm Hg. (This is based on distribution 2 in post number 11.) Based on this information we can assume that the likelihood of getting the observed mean difference of 2 mmHg or something more extreme (i.e. over 2mm Hg) is also 0.0228. It also means that if we assume that the true difference was 2mm Hg then the likelihood of observing the observed result of zero or lower is 0.0228, and above zero it is 0.9772. According to Bayes rule, this means that the prior probability of seeing any observed result above a value X is the same as the prior probability of any true result above a value X. This symmetry and uniformity apply to all the prior probabilities of all true results and all observed results. (This is based on distribution 3 in post number 11.)
The assumption that the directly estimated probability distribution arising from the study is the same as any likelihood distribution based on selecting patients at random from a population of assumed true value (e.g. the null hypothesis of zero) guarantees that scale used for the true and observed values are the same. This can be explained by the fact that the scale of values used for the study are a subset of the universal set of all numbers and that the prior probability conditional on that universal set is the same or uniform or for each of these true and observed values. This uniformity will apply to all studies using numerical values and therefore before any study is even considered. (This is also based on distribution 3 in post number 11.)
We might now explain to the student that a one-sided P value of 0.0228 is the same as the probability of the true result (after repeating the study with an infinite number of hypothetical observations) being the same or more extreme than the null hypothesis. Conversely the probability of the true result being less extreme than the null hypothesis is 1 – P = 1-0.0228 = 0.9772. If the one-sided P value had been 0.025, then it follows from the above that there is a probability of 0.95 that the true result will fall within the 95% confidence interval.
The Bayesian prior probability is different to the above prior probability conditional on the universal set of all numbers. The Bayesian prior will be estimated after designing the study and doing a thought experiment or pilot study to estimate what the distribution of possible results will be in an actual study conditional on background knowledge. This prior distribution can be regarded as a posterior distribution formed by combining a uniform prior distribution conditional on the universal set of all numbers with an estimated likelihood distribution of the thought study result or pilot study result conditional on all possible true values. Each of those latter likelihoods is then multiplied by the likelihood of observing the actual study result conditional on all possible true results. These products are then normalised to give the Bayesian posterior probability of each possible true result conditional on the combined evidence of the result of the Bayesian thought experiment or pilot study and the actual study result. These thought experiments are done to estimate the power required to conduct the actual experiment (e.g. an RCT). However, it is a matter of opinion whether the result of the thought experiment or pilot study should be combined with the result of the actual study.