Statistical conundrum: multiple noisy measurements vs an oracle

[Granville_Matheson]

I have a bit of a statistical conundrum that I can’t quite wrap my head around. It appears very simple, but the results are very counterintuitive, and I just can’t find an intuitive explanation. This all originated with a much more complex model, but I’ve created a very simple example to explain the confusion that I’m having. Any help would be hugely appreciated! I feel like I must be missing something really simple…

Thank you so much in advance for any help!

TL;DR: When testing for group differences in some trait, it seems that using multiple noisy measurements of the underlying trait have better power than using the values handed to us by an oracle.

Scenario

Let’s say we’re examining some property of a bunch of individuals - we can call it IQ for the example. We have two groups: group A and group B, and we wish to examine whether there are differences between these groups. We have 5 different IQ tests which all measure the same underlying trait, but they are all a bit noisy. An oracle then approaches us, and hands us a magical test which tells us exactly what each individual’s true IQ is, with no measurement error at all.

Question

In order to maximise our ability to detect differences between groups, do we A) administer all 5 noisy tests to each individual, or B) administer the single magical oracle test to each individual?

Simulation

I simulated individual true values with a mean and sd. I then simulated 5 measured values per individual with a given measurement error SD around each. I’ve included the code in a gist here: Power Question: multiple noisy measurements vs single noiseless outcome · GitHub

Analysis

I fit four different models to each dataset:

Using one value per individual

I) T-test of the true values
II) T-test of the mean of all 5 measurements

Using multiple values per individual

III) Fixed effects multiple regression: Y ~ 1 + Group + Subj
IV) Linear mixed effects model: Y ~ 1 + Group + (1 | Subj)

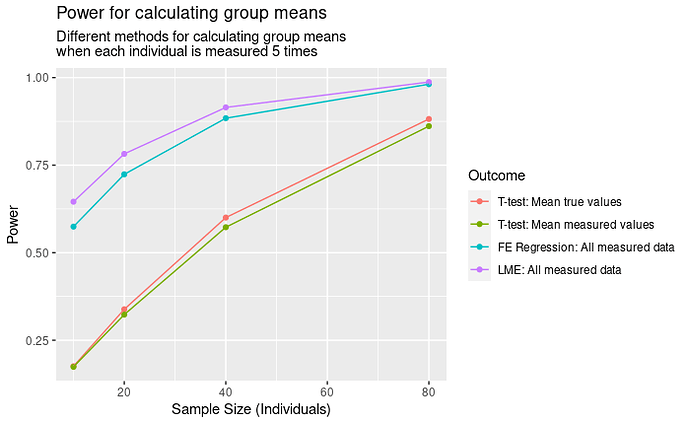
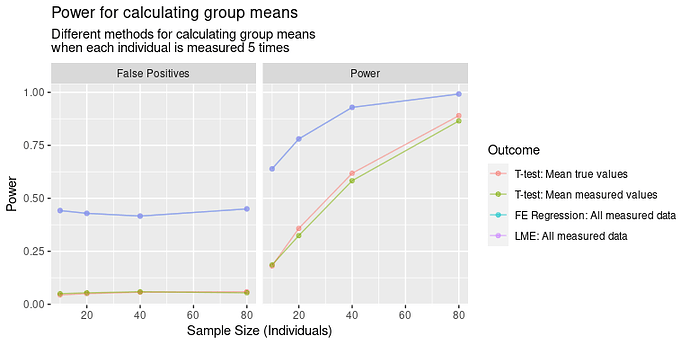
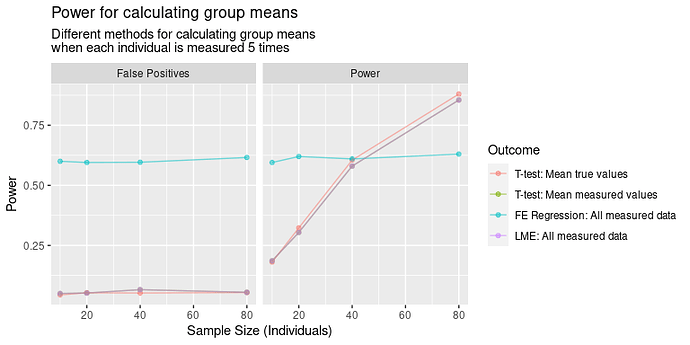
Results

In terms of power, the results are IV > III > I > II. That I is better than II is obvious, but I’m less satisfied with III and IV being better. In this case, we would reject the oracle’s test, and instead choose to measure each individual with our noisy measure? How can this be right?

I understand that we’ve got more samples, so our degrees of freedom are higher, so the SE will be smaller. But it feels extremely counter-intuitive that our model should have better power, without sacrificing type II error rate, for comparisons of multiple noisy measurements compared to the true values. The true population variability remains constant, so there’s always going to be sampling error. And the model examining the true values doesn’t have any measurement error, so the variance should be the correct variance for understanding the sampling variability.

Extension (the more complex model that spawned the question, for those interested)

This all originated in a hierarchical pharmacokinetic model that I’m fitting. We estimate underlying pharmacokinetic parameters (let’s say drug clearance) in two groups of individuals. We usually use models to estimate clearance in each individual from a time series of measurements in each individual, and then compare between groups. I’m now fitting everything simultaneously using a hierarchical model which also includes the group differences in clearance. In simulations, the model appears to exhibit even better power than having the true clearance values themselves. This seems incredibly counter-intuitive, more so than the above example, since we can only learn about the underlying drug clearance from the nonlinear function fit to the whole time-series of values. We expected to get closer to the true values, but we didn’t expect to outperform the true values…

[R_cubed]

I was hoping someone would have answered this, as it occupied my thoughts for a good portion of the day.

Suffice it to say, I think there is a subtle logical contradiction between this narrative:

Blockquote
When testing for group differences in some trait, it seems that using multiple noisy measurements of the underlying trait have better power than using the values handed to us by an oracle.

And this description of the code:

Blockquote
I fit four different models to each dataset:
Using one value per individual
I) T-test of the true values
II) T-test of the mean of all 5 measurements
Using multiple values per individual
III) Fixed effects multiple regression: Y ~ 1 + Group + Subj
IV) Linear mixed effects model: Y ~ 1 + Group + (1 | Subj)

In a paper I’ve mentioned in a number of threads, Bayarryi, Benjamin, Berger, and Sellke describe how a frequentist procedure relates to Bayesian updating with the following equation:
O_{pre} = \frac{\pi_{0}}{\pi_1} \times \frac{(1 - \bar\beta) }{\alpha}

Rejection odds and rejection ratios: A proposal for statistical practice in...

A true statistical oracle, in the above formulation has a \beta = 0 and \alpha \rightarrow 0 for any effect size and sample size.

For an oracle to calculate the 2 sample mean difference, it would only need 2 observations at most (one from each sample). Interestingly, this is also the Hodges-Lehmann estimator that Dr. Harrell mentions frequently in his work.

The oracle formulation places hard constraints on possible samples, as deviations from the true mean need to balance, so that the mean of any 2 observations equals the true mean.

The t-test in the simulations don’t take that information into account. Instead of treating the measurements as ground truth, they treat them as measurements with error.

I’d greatly appreciate it if someone could point out an error in my reasoning.

[MichiganWater]

I don’t speak tidyverse, and speak R at only the beginner level, but I ran your code a few different ways and have a question about this line of code:

simrep = 1:250) %>%

The way I understand how these types of simulations are run is that there will be some number of simulations run (say 1000), and the number of p-values less than 0.05, or the number of times the confidence intervals trap the simulated true value, or something along those lines is calculated and divided by the number of simulations. Am I correct in my interpretation of your code that you want to run 250 simulations, and then see how many of those 250 sims have p-values less than 0.05? So, if 225 of the sims had p<0.05, the power would be 90%.

I changed the 1:250 to 1:2 because I like to see what happens at the extremes, and the observed power should be either 0, 0.50, or 1.0 due to there only being 2 simulations, right? This was not the case when I ran the code with simrep = 1:2) %>%

Hopefully this helps, but, as I said above, there’s a lot in this question/code that I don’t understand, so who knows.

[Granville_Matheson]

@R_cubed : Thank you so much for your response! I think the issue here is that we’re talking about an intermediate oracle. The oracle cannot tell us the means of the two populations. The oracle can only tell us the true individual values. So there is still sampling error to contend with, i.e. when drawing samples from a population, the means will differ from sample to sample.

I think that the t-test in this case is not actually treating these measurements with error. It’s assuming that the SD of the population is what it observes, and it assumes a standard error based on this standard deviation and the number of participants. However, the SD that it is observing has no measurement error, and so there is nothing to disentangle. When there is error, this should increase the total SD: Total Variance = True Variance + Error Variance, and it would then be calculating a new sampling error based on the SD resulting from both noise and error sources. Or am I wrong?

@MichiganWater : Thanks so much for spotting this. I was a bit frustrated at how slowly it was running! I’d left a little bug in the code from a previous iteration, and it was doing many more iterations than I expected. The results remain consistent, but it’s now much faster! You’re absolutely correct regarding your understanding of what’s going on here by the way.

I also got great input from @ngreifer on the Github Gist that I’d embarrassingly forgotten to set the ID as a factor for the FE model, so that’s fixed now too, and there are a few extra sanity checks included.

Addition

I mentioned before initially, incorrectly I now realise, that I was mostly surprised that this occurred with no increase in the type I error rate. I said this because in the complicated model that I mentioned that spawned this question, we see that the type I error rate is still 5%. However, I hadn’t actually specifically checked it in this example, but just assumed it since it was such a basic example. I’ve added this to the simulations and the results are below (after a suggestion on Twitter). I’ve also updated the gist accordingly.

(the LME and FE regression results are overlapping)

We see that actually the LME and the fixed effects regression have greatly increased Type I error rates. So it appears that the mean values and the true values are the only correct methods here. This bugs me even more: I would have thought that the LME model would be the most appropriate model in this situation. Of course, the calculation of p values in LME is hotly debated, so this is why I added the fixed effects regression to compare. What is the correct model to be applying here?? I remember hearing that taking means of values within individuals is problematic because it decreases the SD.

I’m now doubly confused, because the original intent here was to figure out this question to better understand my more complex pharmacokinetic model, but now I realise that they might be relating to slightly different questions. Nevertheless, these results are very confusing indeed, so if anyone has any insights, I’d be eternally grateful!

[ngreifer]

I discovered another error in your code. The same subject numbers are used in both groups! That is, subject 1 has 5 measurements in group 1, but also 5 measurements in group 2. If these are truly meant to be independent groups, then you need to either give the subjects in each group different IDs or use Subj:Group as the grouping variable for the random intercepts. When doing this, we get almost identical p-values between the LME and mean measured values models. These are both higher (i.e., lower power) than the oracle p-values, as we would expect.

My understanding of how to get p-values from mixed models is limited, but it seems that for a between-subjects predictor, the p-value depends only on the variance of the random effect, which is the same as the variance of the residual in the mean measured values model, so the resulting p-values from the two models are the same.

[Granville_Matheson]

Ah, dammit… I’ve been really sloppy here. This changes everything. Thanks for the input! I’ll update in a sec!

[Alireza_Akhondi-Asl]

I think models III and IV are incorrect.
First, I do not understand why you have two groups for each subject. In the current form, each subject has 10 measurements (five for each group), which does not make sense.
Second, in Model III, you are using Subj as an integer in your regression model. This also does not make sense.
Finally, your linear mixed model also seems to be wrong. I don’t think you can model measurement error like this. In LME, each measurement has an independent level I error. But your 5 measurements for each subject have the same level I error. In other words, your 5 measurements are around trueval with the same trueval for all five measurements.

Your models also have some other problems.

[Granville_Matheson]

@Alireza_Akhondi-Asl : Yeah, this was sloppy and unintentional… Sorry for being stupid here. The intention was for each group to be comprised of a different set of individuals, each of whom was measured 5 times. I threw the example together to try to explain the results of a more complex (and more carefully thought-out) model, but I clearly threw it all together a bit too quickly, and made a bunch of really stupid errors along the way. My apologies.

Corrected results

The corrected results show overlap of the mean measured values (II) and LME (IV), FE regression making a dog’s breakfast of everything, and the true oracle values coming out on top.

This is exactly what I would have expected at the start.

So the oracle is, in fact, superior at the end of the day! The correct ordering is I > II & IV > III.

Conclusion

1. I was a bit (not just a bit) sloppy with my code. Thank you so much for everyone who pointed out my errors! I’ve made a bit of an ass of myself here…

2. The oracle is, as originally expected, the optimal solution. The world is as it should be. I will sleep better tonight!

3. I still need to find a good example to relate to my other results not shown here. But there’s a lot more going on there, including a complex nonlinear model with many parameters, Bayesian vs frequentist inference, etc, so there’s a lot more scope for differences to arise.