Dear Colleagues, this is an update to the academic discussion posted on datamethod.org
regarding a secondary analysis of the SPRINT trial(1) did by our research group in Erasmus University Medical Center.[https://journals.lww.com/jhypertension/Fulltext/2019/05000/Impact_of_cumulative_SBP_and_serious_adverse.24.aspx] The core of this post is based on an editorial letter written by Dr. Reboussin and Dr. Whelton (main researchers of SPRINT trial) discussing our methodological approach and results(2) https://journals.lww.com/jhypertension/Citation/2019/08000/Joint_modeling_of_systolic_blood_pressure_and_the.25.aspx. I want to divide this introduction to the discussion into three parts:
1. Why applying joint models for longitudinal and to time-to-event data analysis to SPRINT trial?
The main aim of SPRINT trial(3) was to evaluate if an intensive treatment approach ( lower SBP below 120 mmHg) compared with standard treatment ( maintain SBP between 135-139 mmHg) decrease the hazard to the composite SPRINT primary outcome (Myocardial infarction, other acute coronary syndrome, heart failure, stroke and cardiovascular mortality). The traditional Cox model analysis was the statistical method used in the original SPRINT trial.
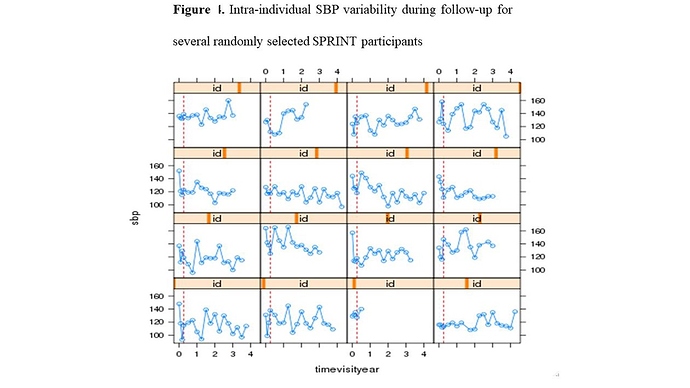
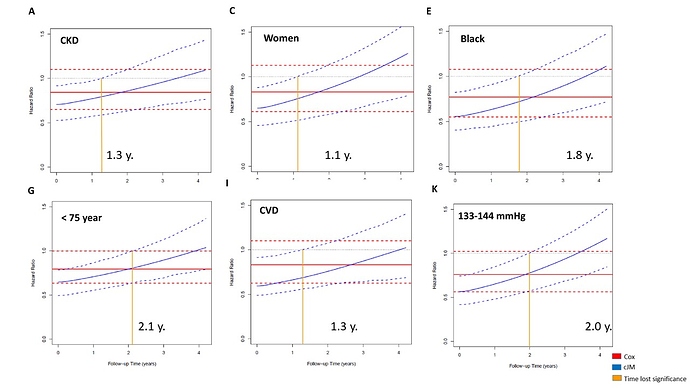
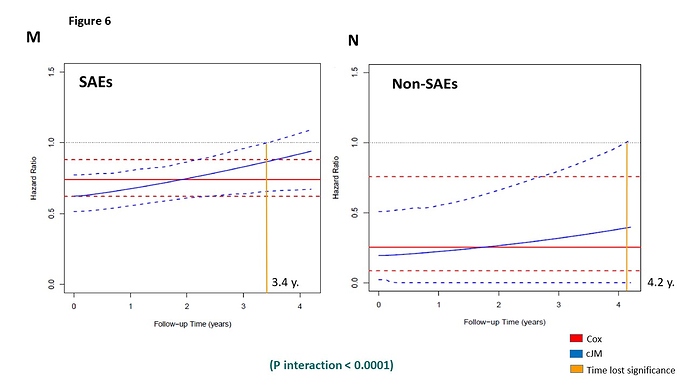
SPRINT trial measured systolic blood pressure (SBP) monthly in the first trimester and then every quarter for 3.26 years median follow-up (range 0 to 4.5 years), in 9361 participants, achieving an average of 15 SBP measurements per person (range: 1-21) during follow-up. This information was not taken into account in the primary SPRINT analysis. Given that: (i) this clinical trial evaluates a strategy of intensive pharmacological intervention (decreasing the SBP <120 mmHg) versus conventional treatment (SBP between 135-139 mmHg), (ii) blood pressure is among the most important risk factor for major cardiovascular events (primary SPRINT outcome), (iii) there is a high SBP variability within the subjects during follow-up (figure 1)
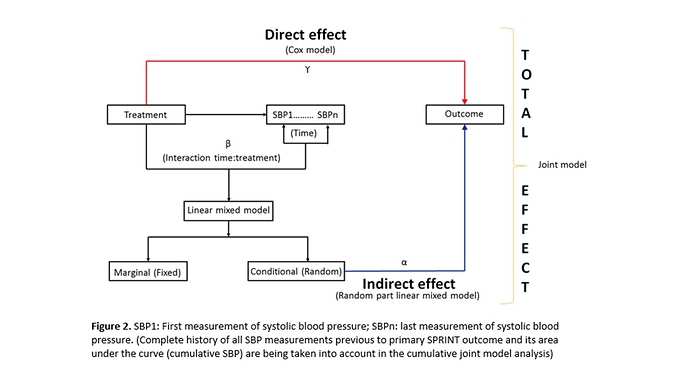
, and (iv) the occurrence of serious adverse events (SAEs) during follow-up can impact both the subsequent SBP figures as well as the primary outcome; a statistical analysis is required that evaluates the impact of longitudinal changes in SBP both within individuals and between intervention groups and takes also the cumulative effect of the SBP on the primary outcome into account (Indirect effect) + the effect of this intervention in the primary SPRINT outcome (Direct effect). This analysis can only be achieved with a statistical model that includes all these elements at the same time, such as the cumulative joint model (cJM) analysis (Figure 2).2. Criticisms of Dr. Rebousssin and Dr. Whelton to our SPRINT secondary analysis (2)https://journals.lww.com/jhypertension/Citation/2019/08000/Joint_modeling_of_systolic_blood_pressure_and_the.25.aspx.
The main concern from Dr. Reboussin and Dr. Whelton to our secondary analysis could be summarized as:
- Analyses of clinical trials that adjust for variables measured after randomization estimate something very different than standard clinical trial analyses which do not employ adjustment or only adjust for baseline variables
- Rueda-Ochoa et al. make a serious error in defining the ‘total treatment effect’ as one that ‘accounts for differences in SBP over time’. In fact, what they report is the component of the intervention effect that excludes the effects produced by changes in SBP. This cannot be viewed as a complete summary of the intervention effect. At best, estimation of this adjusted effect represents a technical accomplishment without clear implications for clinical decision-making.
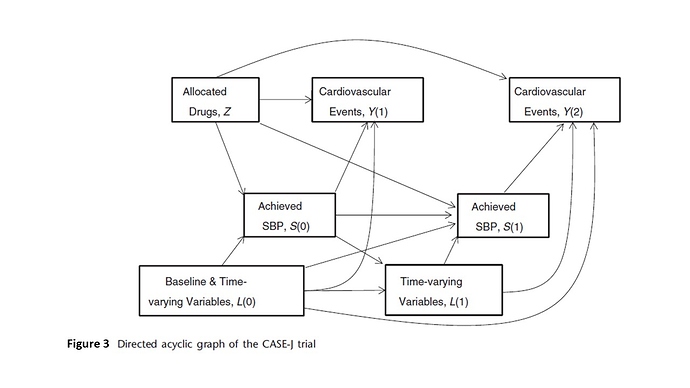
- The Rueda-Ochoa et al secondary SPRINT analysis is similar to the CASE-J trial reported by Oba paper previously published(4) https://www.ncbi.nlm.nih.gov/pubmed/21730076 (Figure 3)
- Compared with the standard intervention, the SPRINT intensive intervention resulted in substantial health benefits, including prevention of CVD events, total mortality, and cognitive impairment that were, if anything, larger later in the follow-up period rather than smaller, as suggested by Rueda-Ochoa et al.
3. Our Reply to Dr. Reboussin and Dr. Whelton editorial letter (4)https://journals.lww.com/jhypertension/Citation/2019/08000/Reply.26.aspx
-
The joint modeling approach does not condition on systolic blood pressure (SBP) after randomization but rather treats it as an outcome. In particular, the joint model uses a linear mixed model for SPB that explicitly allows for different SPB profiles in the two treatment groups. In addition, among others, it accounts for the correlations in the repeated SBP measurements per patient, for missing at random missing data, and the endogenous nature of SPB that relate to the challenges in the interpretation mentioned by Dr. Reboussin and Dr. Whelton.
-
The total effect we have report is the sum of both direct and indirect effect of the intervention. (Figure 2)
-
Our cumulative Joint model analysis is not similar to CASE-J trial analysis in which was used a marginal approach. We used a conditional (mixed ) model approach + Cox proportional hazard model = Joint model analysis. For more detail comparison between these approaches, I recommend Lindsey Jk and Lambert P. paper https://www.ncbi.nlm.nih.gov/pubmed/?term=STATISTICS+IN+MEDICINE%2C+VOL.+17%2C+447%C3%90469+(1998)+Statist.+Med.%2C+17%2C+447%C3%90469+(1998)
-
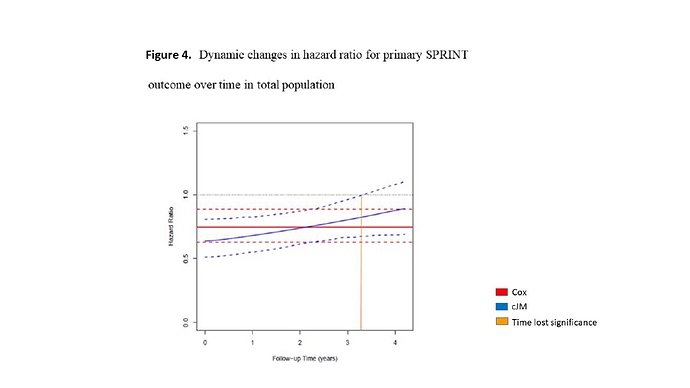
It should be remembered that in the cumulative joint model analysis one takes into account the effect of SBP (cumulative and intra-individual SBP variability) on primary SPRINT outcome and it is not only the marginal difference in events. Clearly, the differences found in the changes over time in the HR in our analysis compared with the number of events marginally reported by Whelton et al can be along the lines of Yule-Simpson´s paradox.
Finally, I would like to invite to all colleagues to contribute in this academic discussion.