I was reminded by @Stephen Senn recently about my comment on Twitter some months ago that risk based models did not seem to work as expected because those with low risk seem to benefit more from treatment than predicted (i.e. more than expected from diagnostic reasoning). For example, statins are expected to reduce CV risk by lowering the cholesterol. Statins should not reduce risk by lowering BP. If the BP is persistently high resulting in high CV risk then statins shouldn’t help and this risk should be tackled with medication to reduce BP such as thiazides, ACE inhibitors, ARBs etc.
If we estimate overall CV risk using the Mayo Clinic Statin Choice Decision Aid for example, in a 65 year old white male when the lipid levels are perfect (high HDL=120 equal to the Total Cholesterol = 120 so that LDL=120-120 = zero) and the only ‘abnormality’ is a high BP of 250 mmHg (i.e. horrendous CV risk), then according to the Mayo risk model, statins dramatically reduce the overall risk from 16% to 10% (a risk reduction of 38%) as if statins had reduced the BP. This is a rather perverse causal inference from a medical point of view.
If the BP is at a perfectly low risk of 100 mmHg systolic and the HDL=10, Total Cholesterol 250 with an LDL=250-10=240 (i.e. a horrendous CV risk) then as expected high dose statins reduce the 10 year risk from 15% to 9% (a risk reduction of 40% similar to that for hypertension). If both risk factors are high risk e.g. the BP is 250 mmHg (i.e. horrendous) and the HDL=10, Total Cholesterol 250 with an LDL=250-10=240 (i.e. also horrendous) then as expected high dose statins reduce the 10 year risk from 55% to 33% (a risk reduction of 40% again as for statins alone).
What seems to be happening here is that the risk reduction of about 40% that applies to one covariate is being applied to other covariates too (including age, acting as an elixir of youth). If a blood pressure lowering agent is added, then this may genuinely reduce the CV risk due to high BP. This will be added to the spurious reduction of BP risk due to the statin thus over-estimating the treatment effect. In short, if the baseline risk is an overall risk based on a number of covariates (e.g. lipids, BP, age, HbA1c, gender etc), the risk reduction from one treatment should be calculated based on the change of risk for its target covariate alone (e.g. HDL, Total Cholesterol and LDL in the case of statins) This might be subtracted from the overall risk (or reduced according to some other mathematical model such as survival from a CV event).
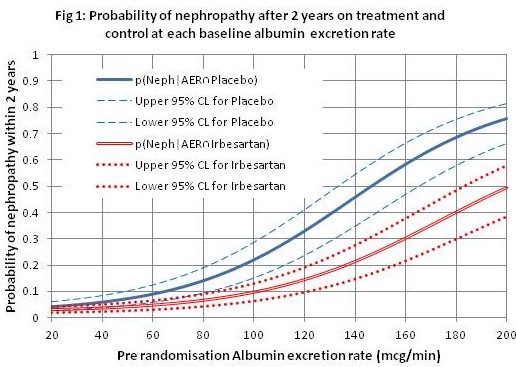
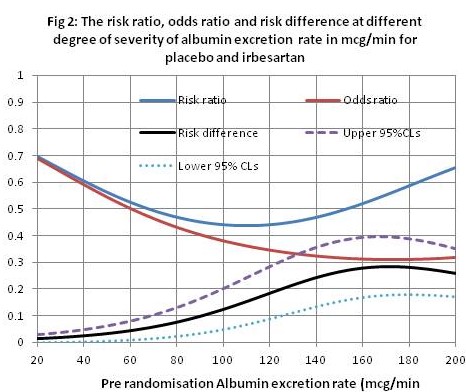
Trying to remedy the above issue creates all sorts of problems and has to involve many more assumptions that include the controversy as to whether we should use risk ratios, odds ratios or switch risk ratios to model treatment effect (discussed at length on DataMethods). I try to avoid the issue by fitting a logistic regression function to the control (placebo) and treatment (irbesartan) data that represent disease severity (albumin excretion rate - AER) in the RCT, instead of only fitting a function to the control data and assuming a constant OR or RR across all degrees of severity to estimate the treatment curve. When functions are fitted in this way (see Figure 1 showing the probabilities of nephropathy conditional on different values of the AER as a measure of disease severity), the OR and RR do not appear to be constant across the range of disease severity (see Figure 2).
This approach represented by Figure 1 can be taken with all the covariates that affect the probability of an outcome (e.g. in the case of nephropathy, the HbA1c that is a reflection of blood sugar control, blood pressure, age, etc.). The probabilities of the outcome conditional on the individual patient’s test result is read off from each curve and substituted for the average ‘prior’ probability before that patient’s current result became known minus the intercept to avoid double counting the effect of other covariates (the intercept is about 0.04 in Figure 1). Instead of adding these individual probabilities (e.g. 0.373, 0.02, 0.107, 0.056 and 0.0069) the product of their complements is calculated (e.g. (1-0.373)(1-0.02)(1-0.107)(1-0.056)(1-0.0069) = 0.514 (the probability of survival from nephropathy), the probability of the outcome of nephropathy being 1-0.514=0.486. I am flying a kite with these calculations in an Excel spreadsheet (accessed via this link: https://osf.io/6k28v for those with the energy, patience and familiarity with Excel). The probability of nephropathy on control and conditional all the simulated covariates was 0.486, reducing to 0.284 (RD=0.202) on two treatment effects applied to their own individual covariates alone read from curves such as that in Figure 2.
I also make some calculations by assuming that the probability of nephropathy as estimated in Figure 1 by the AER is little affected by the other covariates that are represented by the 95% confidence intervals at different degrees of severity. In clinical practice we try to design tests that dominate in this way (e.g. MRI appearances, free thyroid hormone concentrations, AER etc). For example, the probability of nephropathy conditional on control and an AER of 133mcg/min was 0.413, reducing to 0.188 (RD=0.225) on irbesartan alone see Figure 1). This is the approach that I would favour. The problem is that ‘improving’ the prediction by reducing potential bias from other covariates that have less influence on the probability of the outcome (as in the previous paragraph) will also increase the variance of the latter and greatly widen the 95% confidence intervals, thus perhaps being counterproductive. The possible methods like the one suggested by me are also complicated and full of dodgy assumptions.
I also applied the ‘dodgy’ product of two risk ratios to the control probability of nephropathy (in an analogous way to the statin calculation in the third paragraph above). In that case, the probability of nephropathy on control and conditional all the covariates was 0.486 again, but 0.194 (RD=0.292) on the product of two risk ratios applied to all individual covariates. This example exaggerates the risk difference compared to the other two methods as for the statin example in paragraph 3 above.
Perhaps the way to compare these approaches is to calibrate the probabilities of the outcome based on the different methods. I would be grateful for comments and advice about these thoughts.