If I understand, there are 2 remaining issues:
I take your point. I tried to combine the estimated distribution as if it were a Bayesian prior distribution based on knowledge of the proposed study, with the actual result of the first study to get a posterior estimation. I agree that the reasoning doesn’t work in this setting. I will therefore use the term ‘Bayesian-like’ because I don’t intend to use the estimated distribution in a Bayesian manner by combining it with a likelihood distribution to get a posterior distribution. It is the following five approaches (A) to (E) that I am proposing as being legitimate:
(A) To estimate the probability of replication ‘x’ to get P≤y (1 sided) in a second study when the first study’s observations are known already: (i.e. (1) the number ‘n’ of observations made, (2) the observed difference ‘d’ of the mean from zero and (3) the observed standard deviation ‘s’). This approach is based on doubling (*2 in the formula below) the variance being calculated from the above 3 observations.
x = NORMSDIST(d/(((s/n^0.5)^2)*2)^0.5+NORMSINV(y)) Equation 10
(B) To estimate the number of observations ‘n’ needed for a power of ‘x’ to get P≤y (1 sided) in the first study from a ‘Bayesian-like’ prior distribution based on prior knowledge of the planned study that allows an estimate to be made of the difference of the mean from zero ‘d’ and an estimated standard deviation ‘s’. This calculation involves doubling the variance of the Bayesian-like prior distribution (applied by ‘/2’ in the formula below).
n = (s/(((d/(NORMSINV(x)-NORMSINV(y)))^2)/2)^0.5)^2 Equation 11
(C) To estimate the number of observations needed for a power of x to get P≤y 1-sided in the second study from a ‘Bayesian-like’ prior distribution based on an estimated difference of mean from zero ‘d’ and an estimated standard deviation ‘s’. This calculation involves tripling the variance of the Bayesian-like distribution (applied by ‘/3’ in the formula below).
n = (s/(((d/(NORMSINV(x)-NORMSINV(y/2)))^2)/3)^0.5)^2 Equation 12
(D) A ‘what if’ calculation based on the above Bayesian-like distribution by calculating the probability of replication ‘x’ of the first study based on doubling the variance of the Bayesian-like distribution (applied by ‘/2’ in the formula below) and by inserting various observation numbers ‘n’, various values of the difference of the mean from zero (d), the standard deviation (s) and the desired a 1-sided P value ‘y’, into the expression. This can be used for sensitivity analyses of the parameters of the Bayesian distribution.
x = NORMSDIST(d/(((s/n^0.5)^2)*2)^0.5+NORMSINV(y)) Equation 13
(E) A ‘what if’ calculation based on the above Bayesian-like distribution by calculating the probability of replication ‘x’ of the first study based on tripling the variance of the Bayesian-like distribution (applied by ‘/3’ in the formula below) and by inserting various observation numbers ‘n’, various values of the difference of the mean from zero (d), the standard deviation (s) and the desired a 1-sided P value ‘y’, into the expression. This can be used for sensitivity analyses of the parameters of the Bayesian distribution.
x = NORMSDIST(d/(((s/n^0.5)^2)*3)^0.5+NORMSINV(y)) Equation 14
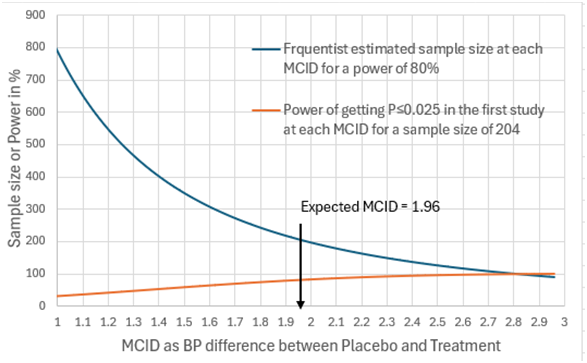
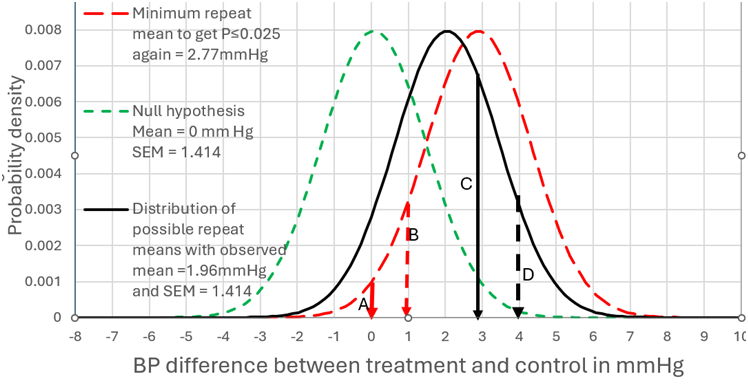
I will address your interesting point about non trivial differences. The best diagram I have is with the example of a mean difference of 1.96mmHg BP difference and a SD of 10. Figure 1 can therefore represent scenario (A) when the number of observations was 100. In this case there was a probability of replication of 0.283 for a one sided P value:
=NORMSDIST(1.96/(((10/100^0.5)^2)*2)^0.5+NORMSINV(0.025)) = 0.283 Equation 15
This corresponds to the area to the right of arrow C of the distribution under the black unbroken line) where P≤0.025 in the replicating study (i.e. all BP differences ≥2.77mmHg).
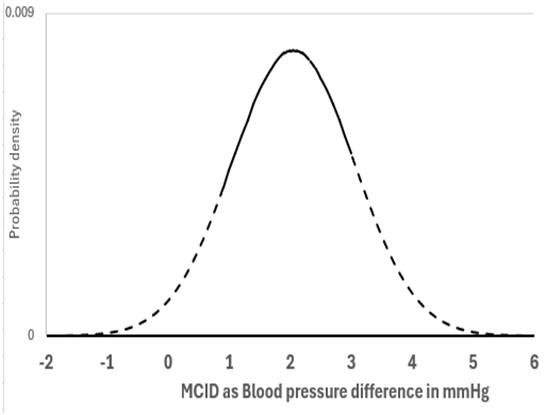
By assuming that the prior probability conditional on the set of all numbers is uniform (i.e. prior to knowing the nature of the study), then when P=0.025, the probability of the true value being a BP difference of ≥0mm Hg is 0.975 (see the area to the right of arrow A in Figure 1 under the green dotted distribution). For a non trivial difference of 1mmHg BP we look at the area to the right of arrow B, where the probability of the true value being a BP difference of ≥1mm Hg is 0.831 and P=0.169 (1-0.831). The probability of getting the same result again is also 0.283.
If we move the arrow C to D (from a BP difference of 2.77mmHg to 3.77mmHg) then this BP difference of ≥3.77mmHg accounts for 10% of the results. They correspond to P≤0.003824 for the green dotted distribution at the broken black arrow D. The probability of the true value being a BP difference of ≥0mm Hg conditional on a result mean of 3.77mmHg is 0.996176 (1-0.003824). This is represented in Figure 1 by moving the red dotted distribution from a mean of 2.77mmHg (the big black arrow) so that the mean is 3.77mmHg (the small broken arrow D). However, the probability of the true value being a BP difference of ≥1mm Hg conditional on an observed mean of 3.77mmHg is 0.975. There is a probability of 0.100 that this will also be the case if the study is repeated (corresponding to the area under the black unbroken distribution to the right of arrow D).
NORMSDIST(1.96/(((10/100^0.5)^2)*2)^0.5+NORMSINV(0.003824))=0.100 Equation 16
Figure 1:
In conclusion, these arguments depend on a number of principles:
Looks good. Just consider using a small prior SD on the true mean difference.
A pure Bayesian look at the problem might be emphasizing Pr(effect > c | study 1 data, prior) and Pr(effect > c | study 1 and study 2 data, prior).
A side remark: Frequentist multiplicity comes largely from asking too little from the data, i.e., trying to get evidence against an exactly zero effect. When you calculate Pr(union of events that are all easy to achieve) e.g. Pr(treatment effect > 0 on one thing or effect > 0 on other thing) this compound probability can easily be high. When you replace 0 with c (c > 0) not so much.
My main point is that the replication crisis might be due to the current frequentist method of estimating sample sizes during power calculations. This is because they appear to underestimate the number of observations required for the first study and do not estimate the numbers required for the second study at all. According to my reasoning if in a crossover study the observed BP difference minus zero was 1.96mmHg with a standard deviation of 10mmHg, then in order to get a one-sided P value of 0.025 or less in the first study, we would require 409 observations by applying double the variance of the prior estimate (‘/2’ below):
(10/(((1.96/(NORMSINV(0.8)-NORMSINV(0.025)))^2)/2)^0.5)^2 = 408.6 Equation 17
However, the conventional frequentist estimate is only based on the (single) variance of the prior distribution (‘/1’ below):
(10/(((1.96/(NORMSINV(0.8)-NORMSINV(0.025)))^2)/1)^0.5)^2 – 204.3 (Equation 18).
Do you think that the results of Pr(effect > c | study 1 data, prior) and Pr(effect > c | study 1 and study 2 data, prior) affect the estimations of the number of observations required according to Equation 17 or Equation 5 (or in general terms Equations 11 and 12)?
Yes I think that would meaningfully affect the calculations. There is also a philosophical question: Should study 2 be informed by any results from study 1? Should a Bayesian approach just treat Study 2 as a continuation of Study 1 so that the posterior can be sharpened (I think so).
Thank you. I suppose the only way to solve the problem is to make different assumptions, calculate the estimated the probability of replication, record how often the replication occurred and then see which calculation resulted in a calibration curve of estimated numbers of observations that was nearest to a line of identity after study similar to that conducted by the Open Science Collaboration!
When Frequentists estimate the number of observations to achieve a specified power of getting P up to a specified value, they too are making a prior subjective estimate based on effect size. However, they do not bring that prior estimate into their calculation by adding its variance to the identical expected variance of the first study. They only base their calculation on the expected variance of that first study based on their prior estimate.
What I propose is basing the estimate of the required number of observations on a ‘double variance’ in a calculation that incorporates the estimated prior distribution. I do not use the term ‘Bayesian’ because the calculation does not use Bayes rule. Instead of a Bayesian multiplication, the calculation involves addition because the second identical probability (not likelihood) distribution is summated on each possible result of the first estimated prior distribution to create a new 3rd distribution with an SEM that is double the original SEM. In order to estimate the probability of replication in a second study the process is continued because the original distribution is summated on each possible result of the 3rd distribution to create a 4th distribution with an SEM that is triple the original SEM. In terms of Bayesian philosophy, I have already incorporated the prior distribution and doing it again may exaggerate the probability of replication.
The Frequentist estimation of the numbers needed to get to get P≤0.25 with a difference of 1.96, a SD of 10 is 204.5. Incorporating the prior distribution gives 2 x 204.5= 409. However in order to get P≤0.25 in the second study, we need 409+204 = 613. If we use the latter during study, then the probability of getting P≤0.25 in the first study is 0.929
= NORMSDIST(1.96/(((10/613^0.5)^2)*2)^0.5+NORMSINV(0.025))= 0.929 (Equation 19). However, the latter takes into account a range of possible P values. If the P value happened to be 0.025 on the basis of 613 observations in the first study, the probability of getting 0.025 again in the second study conditional on this P value in the first study would be 0.929 again, the calculation being identical to Equation 19. Interestingly, if the first study’s P value happened to be 0.054 one-sided, the probability of replication in the second study based on 613 observations in the first study would still be 0.803:
=NORMSDIST(1.6)/(((10/613^0.5)^2)*2)^0.5+NORMSINV(0.025)) = 0.803 (Equation 20)
Because the prior distribution has already been taken into account, I’m not sure that a PLAN to incorporate the prior distribution into a Bayesian calculation could change the numbers required in the study. However, if the effect size and SEM in a completed study were very different to that in the original prior estimate, perhaps Pr(effect > c | study 1 data, prior) and Pr(effect > c | study 1 and study 2 data, prior) should be estimated. Unless there were a very big difference between the effect sizes and SEMs, the impact of the prior distribution might be muted as the number of observations on which the real outcome was based might be 2 or 3 times those in the prior distribution.
There is a related literature on Bayesian sample size estimation with a key word of assurance. They do frequentlist-like calculations but with a continuous distribution for effect size instead of using the single MCID.
Thank you again. I Googled 'Bayesian’ and ‘assurance’ and discovered this paper by Brus et al: Bayesian approach for sample size determination, illustrated with Soil Health Card data of Andhra Pradesh (India) (sciencedirectassets.com). Table 2 of this paper compares the results of applying the Frequentist approach and various Bayesian approaches to estimating sample size. The latter were 5% to 30% higher than the Frequentist estimates. I have not examined the details of the Bayesian calculations but superficially, they do not give similar results to the methods suggested by me and they do not address the issue of replication with a second study. This suggests that the Bayesian and the approach suggested by me for estimating sample size are based on different underlying assumptions.
Yes but it may be possible to blend the two, if it helps. I did one calculation here where replacing a point MCID of 0.65 with a uniform interval 0.55 yo 0.75 resulted in about 0.1 lower “Bayesian power”.
Does the Figure 1 below using my example of BP differences illustrate the same point (if I understand it correctly)?
Figure 1
FWIW, this 2022 paper published in Statistical Science by Micheloud and Held are directly relevant to this thread. Fortunately it is open access.
I think these are single-point-MCID conditional probabilities, no?
Sorry. I should have explained what I did more clearly.
I listed in Excel a range of MCIDs from 0.96 at 0.01 intervals up 2.96 and calculated the sample size required to get P≤0.05 two sided with a power of 80% at each MCID (the blue line in the Figure) using my usual expression:
=(10/(((MCID/(NORMSINV(0.8)-NORMSINV(0.05/2)))^2)/1)^0.5)^2
I then calculated the various powers obtained with the frequentist sample size of 204.3 (based on an assumed MCID of 1.96) for each listed MCID instead, using the expression:
=(NORMSDIST(MCID/(((10/204.3^0.5)^2)*1)^0.5+NORMSINV(0.025)))*100
These calculations were not weighted according to a prior probability distribution of each MCID (their distribution can therefore be regarded as ‘uniform’). However if a prior distribution had been specified, its expected or modal value would have been at 1.96mmHg BP difference. I suppose the prior probabilities of the possible MCIDs would be along the lines of Figure 2 (the dotted points were not in the above calculations, only those between 0.96 and 2.96):
Figure 2
This fixed \alpha and then choose \beta is not consistent with a Bayesian perspective, which minimizes a linear combination of \alpha and \beta.
I’m not sure that I am operating within a Bayesian framework because I don’t use Bayes rule in my calculations. Instead of combining distributions by finding their products, I summate them by adding their variances.
What is wanted is not the MCID that achieves a certain power but rather the average (over MCID distribution, uniform or not) power.
I thought what you meant by this was a form of sensitivity analysis, to show to what extent an estimation of power or sample size could be affected by different estimations of MCID. I was unable to find your calculation in the link that you provided to confirm this, so I tried to do the same using my BP example to see if this is what you meant in the quote. Clearly I had misunderstood. Sorry.
The BP example seemed to be different but maybe I missed something. You can think of this as a sensitivity analysis, or better still as a replacement for that that doesn’t have the subjectivity of how you are influenced by a sensitivity analysis (pick worst case? median case?).
I have been trying to unpick the source of my misunderstanding. I am more familiar with the concept of asking individual patients about what outcome(s) they fear from a diagnosis (e.g. premature death within y years). The severity of the disease postulated by the diagnosis has an important bearing on the probabilities of these outcomes of course. I therefore consider estimates of the probability of the outcome conditional on disease severity with and without treatment (e.g., see Figures 1 and 2 in https://discourse.datamethods.org/t/risk-based-treatment-and-the-validity-of-scales-of-effect/6649?u=huwllewelyn ).
I then discuss at what probability difference the patient would accept the treatment. Initially this would be in the absence of cost and adverse effects to be discussed later, perhaps in an informal decision analysis. If the patient’s choice was 0.22-0.1 = 0.12 (e.g. at a score level of 100 in Figures 1 and 2 above), then this difference could be regarded as the minimum clinically important probability difference (MICIpD for that particular patient. The corresponding score of 100 would be regarded as the minimum clinically important difference (MCID) in the diagnostic test result (e.g. BP) or multivariate score. .
There will be a range of MICpDs and corresponding MICDs for different patients making up a distribution of probabilities and scores. with upper and lower 2 SDs of the score on the X axis on which the probabilities are conditioned. The lower 2SD could be regarded as a the upper end of a reference range that replaces the current ‘normal’ range. This lower 2SD could chosen as the MCID for a population with the diagnosis for RCT planning. For the sake of argument I used such an (unsubstantiated and imaginary) BP difference from zero as an example MCID in my sensitivity analysis. I am aware that there are many different ways of choosing MCIDs of course.
In my ‘power calculations for replication’ I estimate subjectively what I think the probability distribution of a study would be by estimating the BP difference and SD (without considering a MCID). I then calculate the sample size to get a power of replication in the second replicating study. If this estimate was a huge number and unrealistic I might reconsider the RCT design or not do it! The sample size should be triple the conventional Frequentist estimate for the first study. Once some interim results of the first study become known then these can be used to estimate the probability of replication in the second study by using the observed difference and SD so far in that first study and applying twice its variance. Some stopping rule can be applied based on the probability of replication as suggested in the paper flagged by @R_cubed (Power Calculations for Replication Studies (projecteuclid.org) ). The original estimated prior distribution could be combined in a Bayesian manner with the result of the first study to estimate the mean and CI of a posterior distribution. However if I did the same for estimating the probability of replication in the second study, I might over-estimate it. I would be grateful for advice about this.
I will offer an example of the principles discussed in my previous post that outlines a difficult problem faced by primary care physicians in the UK. There is a debate taking place about the feasibility of providing the weight reducing drug Mounjaro (Trzepatide) on the NHS. People without complications of obesity already were recruited into a RCT if they had a BMI of 30 and upwards [1]. The average BMI of those in the trial was 38. On a Mounjaro dose of 5mg weekly, there is a 15% BMI reduction on average over 72 weeks. If the dose was 15mg, there was a 21% BMI reduction. The primary care physicians in the UK are concerned about the numbers of patients that would meet this criterion of a BMI of at least 30 and that their demand for treatment might overwhelm the NHS for questionable gain.
The decision of the patients to accept treatment might depend on the beneficial cosmetic effect of weight reduction. It would be surprising if the NHS could support Mounjaro’s use for this purpose alone. However, it could support a risk reduction in the various complications of obesity that might reduce quality or duration of life and potential for employment. However, this information is not available as the BMI was used as a surrogate for this. The black line in Figure 1 is a personal ‘Bayesian’ estimate (pending availability of updating data) of the probabilities conditional on the BMI of at least one complication of obesity occurring within 10 years in a 50 year old man with no diabetes, or no existing complication attributable to obesity. Figure 1 is based on a logistic regression model.
The blue line in Figure 1 shows the effect on the above probabilities of Mounjaro 5mg injections weekly for 72 weeks reducing the BMI by the average of about 6 at each point on the curve (i.e. 15% at a BMI of 38) as discovered in the trial. This dose shifts the blue line by a BMI of 6 to the right for all points on the curve. The red line shows the effect on these probabilities of Mounjaro 15mg reducing the BMI by 8 at each point on the curve (i.e.by 21% at a BMI average of 38 as discovered in the trial). Shifting the curves by a constant distance at each point on the curve gives the same result as applying the odds ratios for the two doses at a BMI of 38 to each point on the placebo curve.
Figure 1
Figure 2
Figure 2 shows the expected risk reduction on Mounjaro 5 and 15mg weekly at each baseline BMI. The greatest point risk reduction 0.18 is at a BMI of 38. At a BMI of 30, the risk reduction is 0.03. At a BMI of 35, the risk reduction is about 0.12. The dotted black lines in Figures 1 and 2 indicate an estimated ‘Bayesian’ probability distribution (pending updating data) of BMI in the population. Moving the threshold for treatment from 30 to 35 would reduce the populations treated substantially. There will be stochastic variation about these points of course.
Curves such as those in Figures 1 and 2 would have to be developed for each complication of obesity. If a decision to take Mounjaro is shared using a formal decision analysis, the probability of each complication conditional on the individual patients BMI and its utility has to be considered as well as the demands of weekly injections possibly for life. In the USA, this would also involve the cost of medication and medical supervision. The decision analysis would have to compare the expected utilities of Mounjaro, lifestyle modification and no intervention at all.
Is this a fair representation of the difficult problem faced by primary care physicians in the UK when trying to interpret the result of the Mounjaro RCT?