Summary Statistics vs Raw Data

research methods measurement
, , , ,
1

The purpose of this topic is for clinical trialists and statisticians to discuss power, sample size, missing data-handling, and treatment \times time interaction advantages of using longitudinal raw data in analyzing parallel-group randomized clinical trials, as opposed to deriving single-number summaries per patient that are fed into simpler statistical analyses. The goal is to also to discuss challenges to clinical interpretation, and potential solutions. The side issue of statistical volatility problems using sample medians of one-number summaries is also addressed. Emphasis is given to raw data representing discrete longitudinal outcomes.

Consider a therapeutic randomized clinical trial in which time-oriented outcome measurements are made on each patient. Examples include collecting

  • the time from randomization until a single event
  • dates on which a number of different types of events may occur, some of them possibly recurring such as hospitalization
  • longitudinal (serial) continuous, binary, or ordinal measurements taken over a period of months or years, e.g. blood pressure taken monthly
  • serial measurements taken daily or almost daily, e.g., an ordinal response such as the patient being at home, in hospital, in hospital with organ support, or died (we code this here as Y=0, 1, 2, 3).

Some background material:

It is common for clinical trials to use one-number summaries of patient outcomes, for example

  • time to first of several types of events, ignoring events after the first (even if the later event is death)
  • time until the patient reaches a desirable outcome state, e.g., time until recovery
  • count of the number of days a patient is alive and not needing organ support

In the last two categories, occurrence of death presents a complication, requiring sometimes arbitrary choices and making final interpretation difficult. For time to recovery, death is sometimes considered as a competing event. For support-free days, it is conventional in ICU research to count death as -1 days. For computing median support-free days, this is reasonable, but the median is an insensitive measure and has a “jumpy” distribution when there are ties in the data (for continuous Gaussian data, the median is only \frac{2}{\pi} as efficient as the mean, but inclusion of the -1 for death precludes the use of the mean). The median is celebrated because it is robust to “outliers”, but it is not robust to “inliers”; addition of a single patient to the dataset may change the median support-free days by a whole 1d.

Simulations off of an ordinal state transition model fitted to the VIOLET 2 study indicated major power loss when using time to recovery or ventilator/ARDS-free days when compared to a serial Markov ordinal outcome model. In one simulation provided there, the frequentist power of a longitudinal ordinal model was 0.94 when the power of comparing time to recovery was 0.8 and the power of a Wilcoxon test comparing ventilator/ARDS-free days was only 0.3.

Plea: I am in need of individual patient-level data from other studies where a moderately large difference between treatments in support-free days was observed. That would allow fitting a longitudinal model where we know the power of a Wilcoxon test comparing support-free days between treatments is large, and we can determine whether an analysis using all the raw data has even larger power as we guess it would from the VIOLET 2-based simulation.

Another important piece of background information is an assessment of the information content in individual days of outcome measurements within the same patient. An analysis of VIOLET 2 in the above link sheds light on this question. VIOLET 2 had a daily ordinal outcome (not used in the primary analysis) measured daily for days 1-28. I used the first 27 days because of an apparent anomaly in ventilator usage on day 28. For a study with daily data one can ignore selected days to determine the loss of information/precision/power in the overall treatment effect, here measured by a proportional odds model odds ratio (OR) with serial correlation (Markov) structure. Efficiency is measured here by computing the ratio of the variance of the log OR for treatment for one configuration of measurement times compared to another. The configurations studied ranged from one day of measurement at day 14, assessing on days 1 and 27, then on days 1, 14, 27, then 1, 10, 18, 27, then 1, 8, 14, 20, 27, then 1, 6, 11, 17, 22, 27, …, all the way until all 27 daily outcomes are used. The result is below.

image
image983×863 47.2 KB

From the top panel, the effect of using all the daily measurements compared to using the ordinal scale on just day 14 is a 4.7 fold increase in effective sample size. In other words, having 27 measurements on each patient is equivalent to having almost 5 \times the sample size if one compares to measuring the outcome on a single day. It would be interesting to repeat this calculation to compare efficiency with time to recovery and support-free days.

In choosing an outcome for a clinical trial, there are several considerations, such as

  • relevance to patients
  • interpretation by clinicians
  • statistical efficiency
  • ability of the outcome measure to deal with missing or incomplete data
  • elegance with which the outcome measure handles competing/intervening events
  • the ability of the main analysis to be rephrased to provide evidence for efficacy on scales that were not envisioned in the primary analysis

Here I make the claim that analysis of the rawest available form of the data satisfies the maximum number of considerations, and importantly, lowers the sample size needed to achieve a specific Bayesian or frequentist power. This is exceptionally important in a pandemic. Lower sample size translates to faster studies. Even though clinical investigators generally believe that time to event or support-free days are more interpretable, this is only because subtleties such as competing events and missing or censored data are hidden from view, and because they are unaware of problems with sample medians when there are ties in the data.

Another exceptionally important point is that one-number summaries hide from view any time-related treatment effects, and they do not shed any clinical light on the time course of these treatment effects. Analysis of serial patient states can use a model that has time \times treatment interaction that would allow for non-constant treatment effect, e.g., delayed treatment effect or early effect that wanes with follow-up time.

One more advantage of modeling the raw data is that missing or partially observed outcome components can be handled in a way that fully respects exactly what was incomplete in the patient’s outcome assessment. For example, if a patient was known to be alive in the hospital on day 6 but organ support was not assessed on day 6, Y is interval censored in [1,2] and the ordinal model’s log likelihood component for that patient-day will use exactly that. On the other hand, how to handle intermediate missing data in time to recovery or support-free days is not clear.

It is important to describe how results of a raw-data-based analysis can be presented. Let’s consider the case where the daily observations are Y=0,1,2,3 as mentioned above. Note that organ support (Y=2) could be further divided into different levels of support that would result in breaking ties in Y=2. I don’t consider that here. Here are some possibilities for reporting results.

  • If the serial measurements are modeled with a proportional odds ordinal logistic model, whether using random effects or Markov models to handle within-patient correlation, some consumers of the research will find an odds ratio interpretable. The OR in this context is interpreted the same as the OR in an RCT with a simple binary outcome, it’s just that the outcome being described is outcome level y or worse. If proportional odds holds and the outcome is Y=0,1,2,3, the treatment B : treatment A OR is the odds that a treatment B patient is on organ support or dies divided by the odds that a treatment A patient is on organ support or dies, and is also the odds of dying under B divided by the odds of dying under A. Note odds = P(Y \geq y | treatment) / P(Y < y | treatment)].
  • Even if proportional odds is severely violated, the Wilcoxon test statistic, when scaled to be the 0-1 probability of concordance, is \frac{\mathrm{OR}^{0.66}}{1 + \mathrm{OR}^{0.66}}. So the OR is easily translated into the probability that a randomly chosen patient getting treatment B will have a worse outcome than a randomly chosen patient getting A, the so-called probability index or P(B > A).
  • Clinicians who like count summaries such as number of support free days will like the expected time in a given state or range of states that comes from a serial state transition ordinal model. For example, one can compute (and get uncertainty intervals for) the expected number of days alive and on a ventilator by treatment (the mean works well because -1 is not being averaged in), the expected number of days alive in hospital and not on organ support, and any other desired count.
  • Natural to many clinicians will be the probability of being in outcome state y or worse as a function of time and treatment (see graph below). This is a function of OR, the proportional odds model intercepts, time, and the serial dependence parameters.
  • Equally natural are daily split bar charts showing how treatment B possibly redistributes the proportion of patients in the different outcome states, over time (see below).
  • When using a day-to-day state transition model such as a first-order ordinal Markov model, some clinicians will be interested in state transition probabilities. For example one can easily estimate the probability that a patient on a given treatment who is on ventilator one day will be alive and off ventilator the next day. One can also gain insight by estimating the probability that a patient will return to hospital after being at home 1, 2, 3, …, days, or the probability that a patient will again need a ventilator after going off ventilator.

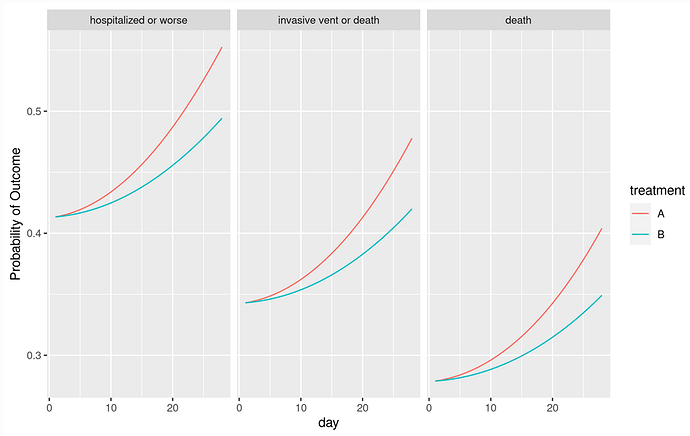
Here is an example of presenting three outcome probabilities as a function of time and treatment. The model contained a linear time \times treatment interaction, with the treatment having no immediate effect.

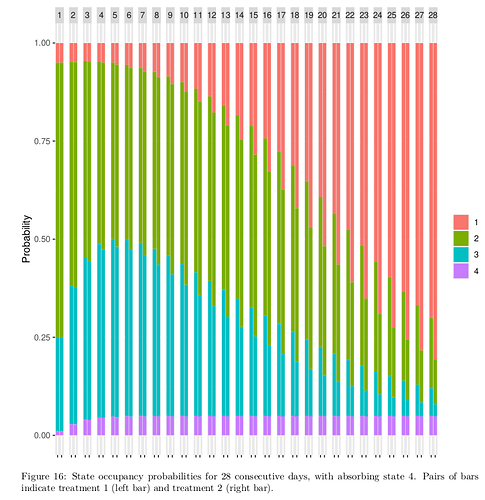
image
image965×611 68.4 KB

Here is a state occupancy probability graph that is becoming more popular in journal articles. TIme is shown at the top, and probabilities for each of two treatments are shown in each pair of bars. This was constructed when the outcomes were coded Y=1,2,3,4.

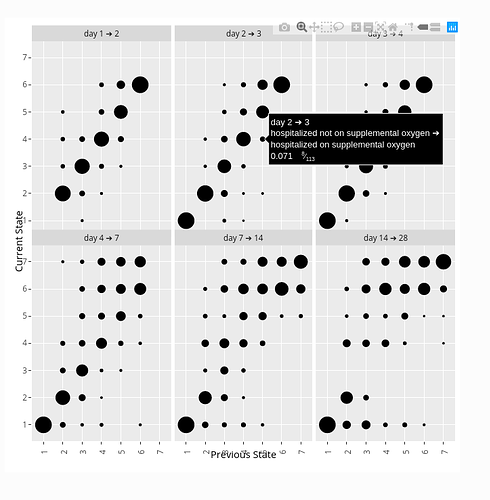
image
image754×777 34.2 KB

Here is a snapshot of an interactive state transition chart from the ORCHID study. Go to the link to see how hovering your pointer displays transition details. Transition charts are not “intention to treat” since they represent post-randomization conditional probabilities (much as hazard ratios in Cox models with time-dependent covariates) so they are not featured for final efficacy assessment. But transition charts are closest to the raw data by completely respecting the study design, i.e., by connecting outcomes within individual patients. Thus state transition tendencies are the most mechanistically insightful ways to present discrete longitudinal data.

image
image725×739 38.2 KB

I argue that

  • ordinal longitudinal models are versatile, providing many types of displays of efficacy results as shown in the graphs above
  • by using the raw data (other than a slight loss of information when two events occur on the same day, as only the more severe event is used), ordinal longitudinal models such as proportional odds state transition models increase power and thus lower sample size when compared to two-group comparisons of over-time summary indexes
  • the types of result displays shown here are actually more clinically interpretable than replacing raw data with one-number summaries, because there are no hidden conditions lurking about, such as missing data or intervening events that interrupt the assessment of the main event of interest

I hope that we can have a robust discussion here, and I would especially appreciate clinical investigators posting comments and questions here. Particular questions about longitudinal ordinal analysis will help us better describe the method.

Resources

6 Likes
2

Thanks for sharing these thoughts. I agree that the ordinal odds ratio is no real barrier to interpretability. It’s no more difficult to interpret than, e.g., the ED95 or other pharmacokinetic parameters that are commonly used for regulatory approval purposes.

Regarding the following points:

… one-number summaries … do not shed any clinical light on the time course of these treatment effects

This is true, of course, but a trialist may argue that a single number summary, e.g., organ support at 28 days may indirectly encode the notion that differences at earlier time points are not clinically important, or that organ support at 28 days (but not earlier) is reflective of persistent complications. In other words, any differences that may occur prior to 28 days should not be counted in evaluating efficacy of a therapeutic.

… missing or partially observed outcome components can be handled in a way that fully respects exactly what was incomplete in the patient’s outcome assessment. … On the other hand, how to handle intermediate missing data in time to recovery or support-free days is not clear.

Suppose a patient is never observed to receive organ support, is lost to follow-up at day 10 of a 28 day follow-up period, but is known to be alive after 28 days (e.g., did not appear on a death registry). We would know that this patient’s organ support-free days was >=10. It seems that the ordinal model is equally capable of encoding this type of censoring, i.e., the organ support-free days is censored in the interval [10-28].

Thanks again!

1 Like
3

Nice thoughts Matt. I think that the “raw data” approach provides both efficacy measures of clinical relevance (e.g., probability of being alive and support-free at 28d) and especially sheds light on the treatment-outcome process (shape and slope of the outcome tendencies over time).

That’s a good point. The problem may come into play more so when there are more categories for the patient needing support with missing assessments on some of them. An overriding issue is how to summarize support-free days even without censoring. You can’t use the central tendency measure that is most compatible with the Wilcoxon test—the Hodges Lehman estimator—because it doesn’t work when there are many ties. The ordinary median doesn’t work with ties, and the mean can’t be used because of the -1 values. To me this is a vote for focusing on quantities such as the probability of not needing organ support and being alive at 10d, i.e., you can compute probabilities about things whether those things have tied values or not.

1 Like
4

“Summary Stats vs Raw Data” seems to me an example of ‘epistemological dIchotomania’. What about Latent Variables? Admitting these into the discussion would actually allow you to frame it in the more general terms of state-space modeling and data assimilation. Your focus on ordinal state variables could then be examined as an approximation to the more general case of state in \mathbb{R}^n, and the scientific costs of that approximation appreciated.

5

I like variables I can “see” and have managed to solve a variety of problems without using latent variables. :smiley:

2 Likes
6

Ernst Mach (1897): “I don’t believe atoms exist!”
Biostats (2021): “We don’t believe latent variables exist!”

2 Likes
7

Trying to understand the gist of this post at a (sadly) very rudimentary level, coming from a non-stats background. Would these be reasonable “take-away” messages for clinicians (or is this interpretation completely mangled)?:

  • In the context of small sample size (often true for critical care trials), relying solely on assessment of traditional endpoints (e.g., mortality) to assess treatment efficacy is like doing archaeology with a bulldozer rather than a hammer and chisel (?) It’s the wrong tool for the job- lots of good stuff can get tossed aside (?);
  • When sample sizes are constrained, critical care trials might not accrue a sufficient number of outcomes that doctors and patients tend to care about most (e.g, death) to permit a confident inference about a new treatment’s effect on mortality. Two possible solutions:
    1. Don’t run small critical care trials; OR
    2. Try to squeeze as much useful information as possible out of smaller trials, with the goal of identifying those therapies that hold sufficient promise to warrant a larger trial;
  • Changing the way that smaller trials are analyzed statistically might allow for identification of efficacy signals that would otherwise be missed with a continued focus solely on “higher-level” endpoints like death (which can be an insensitive measure of treatment efficacy in settings of restricted sample size);
  • Examining multiple raw clinical parameters from critical care trials and how they change over time could provide a powerful way to show patients’ responsiveness to a new therapy in the context of constrained sample sizes. Identifying such efficacy signals could prevent premature discarding of promising therapies.

Is it reasonable to say that if we don’t observe many deaths in a trial, we will remain hard pressed to make a confident inference about the effect of the treatment on mortality, regardless of how granular our analysis has been? In this context, would the main value of the more granular analysis be revelation of efficacy signals that might be missed by relying on an overly “blunt” indicator like mortality(?) And if even a granular analysis of a small trial fails to reveal a separation between drug-treated and placebo-treated patients with regard to various clinical parameters, maybe we can have added confidence in discarding the therapy (?)

8

You have brought out many great things to discuss, and I hope that you and other non-statisticians will post more discussions like this on this datamethods topic. Here are a few thoughts in response.

  • My post is mainly related to situations where composite outcomes are already of interest, and one wishes to maximize the information content and statistical power in the multiple-outcome data. In cardiovascular research, MACE (major adverse cardiac events such as CV death, MI, hospitalization for heart failure) is commonly used, although the only information that is usually retained in the primary analysis is the time until the first MACE, and this even ignores death after a nonfatal event. We can do much better than that. In critical care research, anyone using ventilator-free days has already decided that ventilation is a valid endpoint. The question is whether one analyzes ventilator free days or analyzes outcomes for 10 consecutive days that look like 0000110112 (death on day 10, 4 days on vent).
  • The methods I outline apply to both small and large trials, and in some cases would allow large trials to become smaller trials, with equal power.
  • Using the most sensitive analysis, and finding evidence against a clinically meaningful effect, allows one to feel more confident in discarding a therapy. All too many clinical trials have been interpreted as “negative” when the endpoint was too insensitive.
  • There are only two ways I know that hitting an evidence target for a compound endpoint can lead one to conclude there is evidence for a mortality reduction. (1) When the nonfatal event added into the mix solidly predicts death, just not death within the time frame of the trial’s follow-up. If the nonfatal event is one requiring rescue therapy (a therapy not being randomized) and without the rescue the patient would have died, one could also make a strong argument for a mortality-related clinical benefit. (2) If efficacy information from the nonfatal events is allowed to be borrowed in a mortality reduction assessment.

On the last point, this discusses how the partial proportional odds model can be used to borrow information from efficacy on nonfatal outcomes towards evidence for mortality. If the clinical experts and regulatory authorities can agree on the prior distribution for the differential treatment effect, and this prior distribution puts more probability on small differential benefit, then the nonfatal events boost the power of the mortality assessment. That will sound foreign to many. Here’s how it works. For the proportional odds ordinal logistic model one has an odds ratio (OR) for the effect of treatment on all outcomes. The partial proportional odds model adds an extra parameter for the differential or “extra” treatment effect on the worst level of the ordinal outcome variable, death. The anti-log of this new parameter is the ratio of odds ratios for the treatment’s unique effect on death to the odds ratio for the treatment’s general effect on all outcome levels. A prior distribution for this ratio of ratios might be stated as “we believe before the study that the probability that the OR for death differs from the OR for all event types by more than a fold change of 1.25 is 0.2”. One uses this prior to compute the posterior probability of a mortality reduction (OR < 1) for the new treatment. To me this more continuous approach is advantageous to looking at mortality in isolation.

Finally, we need to further discuss why a compound outcome is used in a primary efficacy assessment. The primary consideration is that the events that are part of the assessment are important to public health, patients, and physicians. Clinicians must believe that the nonfatal events should be factored into net clinical benefit. In many cases, it’s not just whether or not a patient died; it’s how close to death did she come, and whether she required a risky rescue therapy that like mechanical ventilation may have long-term consequences.

6 Likes
9

Nice to see ordinal analyses being recommended in the neurological literature. They made a few inaccurate statements by not recognizing WMW is a special case of proportional odds (leading to the excessive skepticism about proportional odds assumption), but the major points are correct and important. I’m surprised none of Frank’s work was cited.

2 Likes
10

Hi, Dr. Harrell:

When I tried to replicate the case study in “22 Semiparametric Ordinal Longitudinal Models”, it seems that this line

“vcorr ← readRDS(‘markov-vcorr.rds’)”
did not work on my end, and I was told

"Error in gzfile(file, “rb”) : cannot open the connection
In addition: Warning message:
In gzfile(file, “rb”) :
cannot open compressed file ‘markov-vcorr.rds’, probable reason ‘No such file or directory’ ".

So where could I find this file?

Thanks.