I’m not sure whether what I am about to describe qualifies as an example of solid causal inferences from purely observational data. It is very much based on my understanding of causal reasoning linking diagnostic tests and treatment so here goes and please be sympathetic! Perhaps someone could help me to express my thoughts with DAGs.
I don’t think that a passive instrument that would avoid having to perform a RCT on a treatment (e.g. a randomly occurring birth month used by Angrist and Imbens) would be available very often during many observational studies. In addition, it is important to be disciplined and structured when gathering data. I think therefore that we should also have ‘structured instruments’ under our own control that provide a similar result to randomisation to a treatment or control. I suggest that this can be done by randomising to two different ‘predictive’ or diagnostic tests (or to two different numerical thresholds of one test). Not only can this tell us the efficacy of the treatment but also the performance of the test(s).
I will use example data from a population of patients with diabetes and suspected renal disease, the test being the albumin excretion rate (AER), the treatment being irbesartan that helps to heal the kidney and thus reducing protein leakage. The patients are then randomised to an AER to be used with a test result threshold of 40mcg/min or to be used with a threshold of 80mcg/min. Therefore, the first negative dichotomous test result used (T1 Negative in Figure 1 below) was albumin excretion rate (AER) of ≤ 80mcg/min, the first positive (T1 Positive ) an AER of >80mcg/min. The second dichotomous negative test result (T2 Negative) used was AER≤40mcg/min, the second positive result (T2 Positive) an AER >40mcg/min. Those patients positive for T1 and T2 were treated with irbesartan and those T1 and T2 negative were allocated to control as shown in Figure 1.

Figure 1: Diagram of randomisation to different tests and allocation to control if a test is negative or to intervention if the test is positive
The proportion ‘a’ was that developing the outcome (e.g. nephropathy) and who had also tested negative for T1 (e.g. an AER≤80mcg/min) conditional on all those tested with T1 after randomisation. Proportion ‘b’ was that with nephropathy that had also tested positive (e.g. an AER>80mcg/min) conditional on T1 being performed. Proportion ‘c’ was that with nephropathy that had also tested negative (e.g. an AER≤40mcg/min) conditional on T2 being performed. Proportion‘d’ was that with nephropathy that had also tested positive (e.g. an AER>40mcg/min) conditional on T2 being performed.
If ‘y’ is the probability of the outcome alone (e.g. nephropathy), conditional on those randomised to T1 or T2 then according to exchangeability following randomisation, ‘y’ has to be the same in both groups allocated to T1 and T2, and so:
When ‘r’ is the risk ratio of the outcome on treatment and control (assumed to be the same for those randomised to T1 and T2), the probability of having the outcome when randomised to Test 1 is y = a + a*r +b/r + b.
The probability of having the outcome when randomised to Test 2 is also y = c + c*r +d/r + d
Solving these simultaneous equations gives the risk ratio r = (d-b)/(a-c) .
Therefore when:
The proportion with nephropathy in those T1 negative (AER ≤80mcg/min) = a = 0.050
The proportion with nephropathy in those T1 positive (AER >80mcg/min) = b = 0.0475
The proportion with nephropathy in those T2 negative (AER ≤40mcg/min) = c = 0.0050
The proportion with nephropathy in those T2 positive (AER >40mcg/min) = d = 0.0700
The estimated Risk Ratio = r = (d-b)/(a-c) = (0.07-0.0475)/(0.05-0.005) = 0.5.
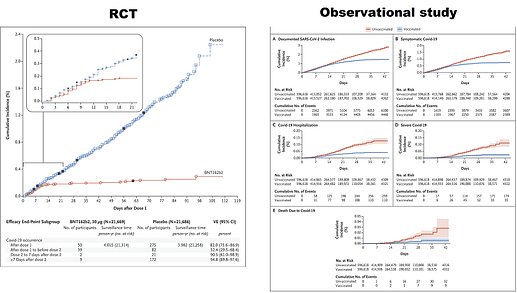
The overall RR based on all the data in the RCT was (29/375)/(30/196) = 0.505.
Note that proportions a, b, c and d are marginal proportions conditional on the two universal sets T1 and T2 (e.g. b = p(Nephropathy ∩ AER positive | Universal set T1)). The conditional probabilities (e.g. p(Nephropathy|AERpositive)) do not feature in the above reasoning. It was assumed also that that the likelihoods (e.g. p(AERpositive|Nephropathy) were the same for those on treatment and control in sets T1 and T2.
It should also be noted that this approach estimates the Risk Ratio in a region of subjective equipoise based on the uncertainty of whether the decision to treat patients should be based on an AER >40mcg/min or AER>80mcg/min. The data was sparse, but fortuitously for this data set, the proportions were Pr(Neph|AER=40-80mcg/min and on Placebo) = 9/199 and Pr(Neph|AER=40-80mcg/min and on Irbesartan) = 9/398. These small numbers merely illustrate the calculation. Normally a very large number of subjects would be required for meaningful estimates. However, as these patients would be under normal care (thus allowing large numbers of patients to be studied), all those who had an AER>80mcg/min would all be treated with Irbesartan and those with an AER< 40mcg/min would not be treated, which would improve the numbers consenting (few might agree to be randomised to no treatment if they has high AER levels).
This type of study with large numbers could be performed during day to day care by the laboratory randomly printing on the test results as follows: “Treat if AER > 40mcg/min” or “Treat if AER >80mcg/min”. Alternatively the laboratory or clinician could allocate to T1 if the patient was born on an odd numbered month (i.e. January, March, May, July, September or November) or T2 if born on the other even numbered months. (This would honour Angrist’s and Imbens’s choice of instrument based on which month students were born!)
The same approach could be taken with two different tests (e.g. RT-PCR and Lateral Flow Device (LFD) for Covid-19). The patients would be randomised to RT-PCR testing or LFD testing and the same design used. In this case the assumed equipoise would be that group of patients who were RT-PCR positive but LFD negative and also those who are RT-PCR negative and LFD positive. This means that all those both RT-PCR positive and LFD positive would be treated (e.g. with an antiviral agent or isolation) as this would only be acceptable to those consenting to the study, but all those RT-PCR negative and LFD negative would not be treated.
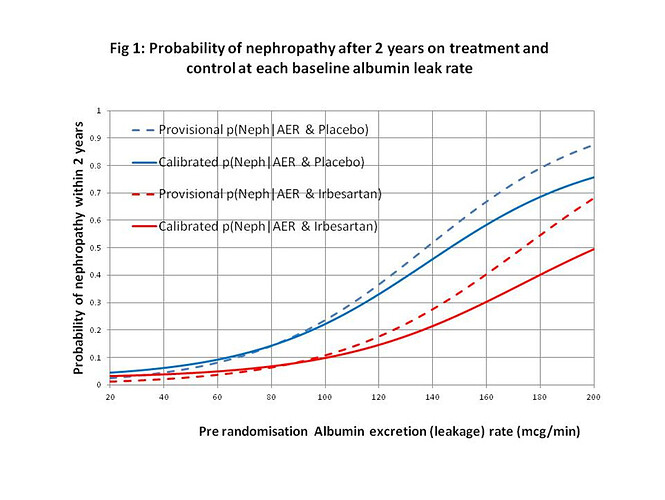
I would regard this approach as a phase 3 observational study that should only be done for a new treatment after the latter’s efficacy has been established with a suitably powered RCT, perhaps for patients with AERs in the range of 40 to 80mcg/min. By also treating or not treating patients outside this range of equipoise, the data could also be used to create curves displaying the probabilities of nephropathy for each value of AER in those treated and on control by using calibrated logistic regression. This would allow optimum thresholds for diagnosis and offering treatment to be established in an evidence-based way (see Figure 2).

Figure 2: Estimated probabilities of biochemical nephropathy after 2 years on placebo and Irbesartan