No problem at all. I know what you meant, and am thankful you brought it to attention, as I may utilize in the future if journals demur on publishing letters that point out major flaws in their publications. I do hope to persuade editors in some cases that “look, publishing a letter would be better for my CV, but a retraction would be better for science.”
Apologies that we are a little off-topic on “Observed Power.” Thus ends this threadjack.
I’d like to offer a challenge that might be helpful in reaching your true audience: surgeons. I cannot believe this issue is so complex as to require such a lengthy and elaborate discussion. I have to think that you could build a Shiny app, and make a 140-second (tweetable) video that demolishes post hoc power for all time. (This might make a nice project for a graduate student, who could even gain some social-media exposure out of it, plus the opportunity to develop and demonstrate statistical teaching/communication/outreach skills.)
Even surgeons and surgeons-in-training will have time for a 140-second video, especially if it criticizes some of their prominent colleagues. As an example of what’s possible in this medium, under its severe constraints, consider this 127-second video produced by yours truly.
In some ways, this has already been done (maybe not the “video” part, but blog posts with a single Figure/simulation that explain it). The problem - at least insofar as I can see - is that understanding that single Figure or simulation still requires an understanding of what statistical power is in the first place, and that absent that understanding, no single Figure or simulation gets it across. So I do not believe, or at least I’m not easily capable of meeting this goal:
I would be more than delighted if you are able to do this. I honestly don’t think that I can.
The surgeons’ interpretation is clearly wrong, but they’ve also been told that in myriad different ways by at least four different replies to their initial publication, and the response was essentially “Thanks, but we’re still right.” If you’ve got a better way to convey this, by all means, go for it.
I guess that’s throwing down the gauntlet, then, and I’ll have to look into it properly. Would you offer a link to the single, most concise—even if ‘incomplete’—treatment you’ve seen so far?
On my phone right now, but Daniel Lakens’ blog post, Russ Lenth’s article and the “Abuse of Power” article (all linked in my PubPeer comment, and all listed in the post above) all include a simple Figure and simulation that should make it clear that “observed power” is just the “p-value from a different angle” (nor is it a number that makes much sense, if one actually understands what it is).
i think the most concise and clear example is the one that says if you get pvalue=0.05 and then calculate posthoc power youll get 50%. Tell that to any clinical personal and theyll recoil
…or they’ll say “see, that’s why we need to lower the standard for power from 80 percent! Even studies with p=0.05 don’t achieve 80 percent power! From now on let’s use 50 percent power!”
Darkness cannot drive out darkness; only light can do that.
Hate cannot drive out hate; only love can do that.— MLK
In all seriousness, I wish to ‘preregister’ the conjecture that what’s most needed is a sympathetic reading of Bababekov et al. That is, I suspect the ‘debunking’ has to begin with an appreciation for whatever legitimate aim they were hoping to achieve.
i hadn’t though of that, youre probably right 
I’ve actually tried that. In the letter that @zad and I submitted in response to their prior paper at Annals of Surgery - which has been accepted but is not yet in print, b/c according to the journal it has been sent to the authors so they can reply (again!) - we offered a better solution for what they’re proposing - namely, that rather than computing an “observed power” based on the study effect size, that they could report the “power” the study would’ve had to detect a modest difference that may have been clinically relevant, with an example. I’m on my phone right now and don’t have that full paper handy, but appreciate what you say and would note that we, along with the others who responded to their initial papers (Gelman in particular) tried to tell them “we get what you’re going for, but this is the wrong way to do it; here’s a (slightly) better way.” This has, to my mind, been tried. Again, if you feel that you have a better way of reaching them, I would be MORE than happy if you can achieve this.
Thanks, I didn’t know that Epidemiology had such a policy. Will submit the rejected LTE there and see what happens.
I also ended up responding on PubPeer to the paper put out by Bababekov et al. (comment awaiting moderation), but here it is:
"Despite statisticians warning against the use of observed power for decades (Hoenig & Heisey, 2001), the practice continues, usually from research groups who are unaware of the problems with it. Bababekov et al. (the authors of this paper) have not only defended their use of observed power in previous papers, even when criticized by statisticians who have looked into the problem, but unfortunately, they encourage others in surgical science to do the same.
The arguments put forth in this paper have no mathematical or empirical basis. Meaning, Bababekov et al. have not given any mathematical proofs or simulated data to make their case. Their argument merely consists of,
“Although it has been argued that P value and post hoc power based on observed effect size are mathematically redundant; we assert that being redundant is not the same as being incorrect.”
“We believe this redundancy is necessary in the unique case of surgical science, as post hoc power improves the communication of results by supplementing information provided by the P value.(12) Moreover, post hoc power provides a single metric to help readers better appreciate the limitation of a study.”
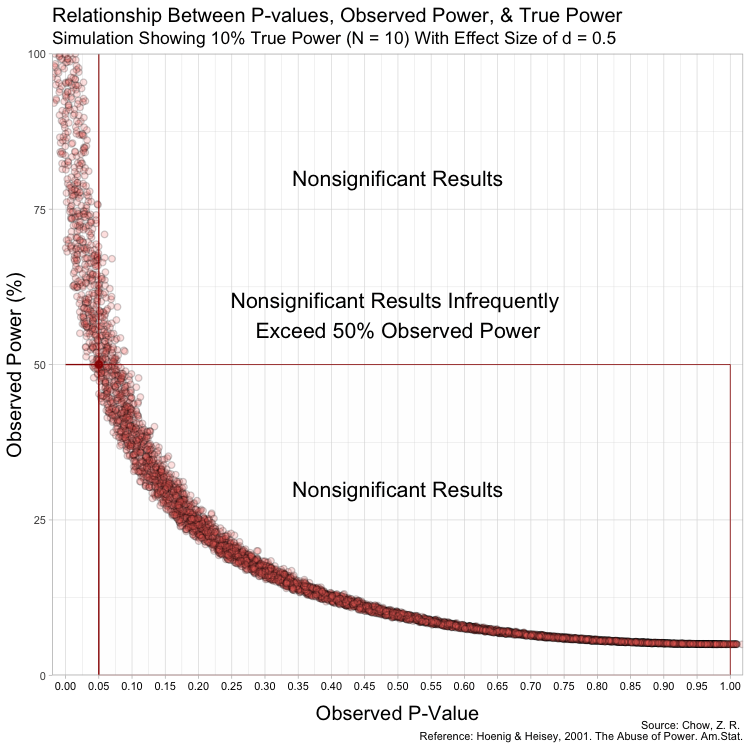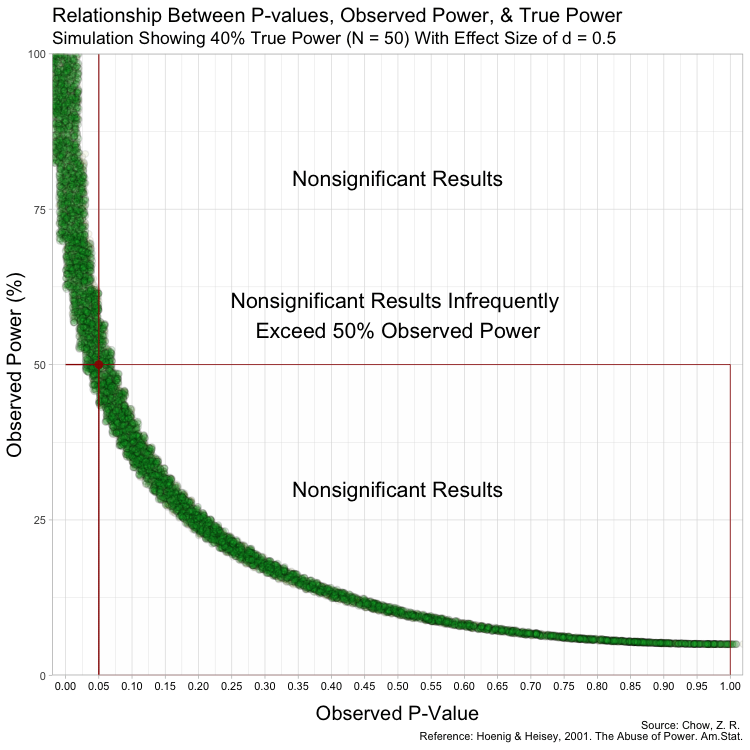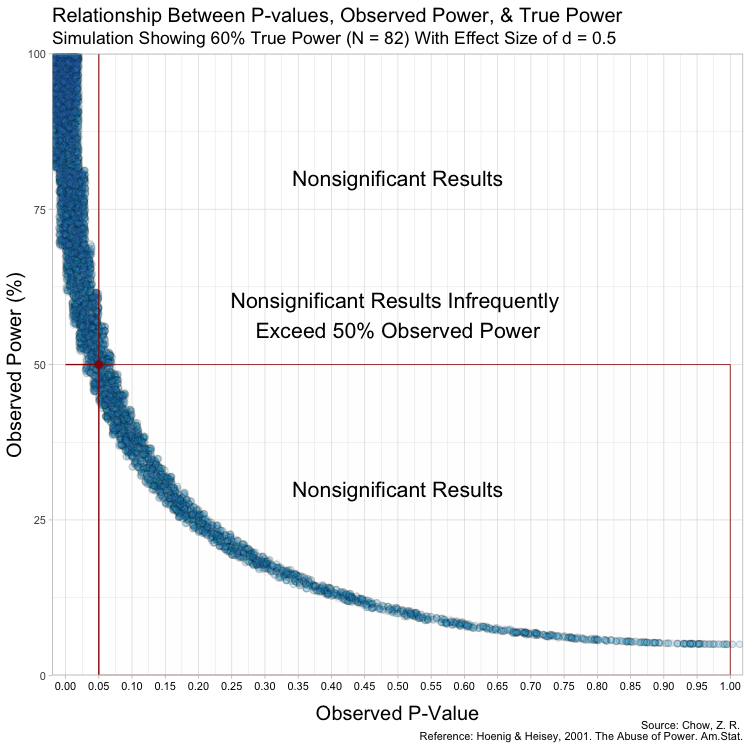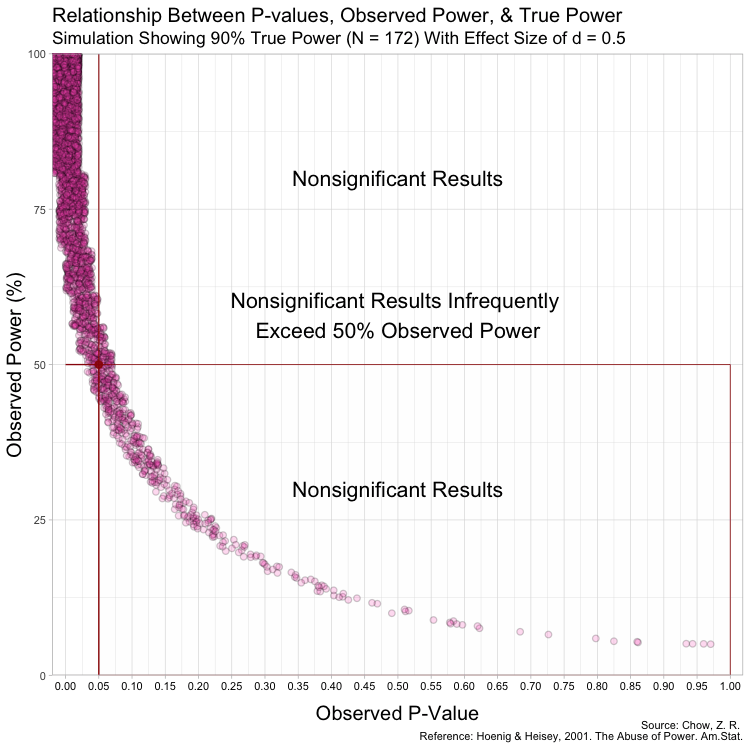
The problem is that this practice is not only redundant, it is incorrect and highly misleading. This can easily be shown with simulated data (see attached image). Here, I simulate 45,000 studies from a normal distribution and where I have set a true between-group difference of d = 0.5.
Group A has a mean of 25 and standard deviation of 10, and group B has a mean of 20 and also a standard deviation of 10. Thus, (25-20)/10 gives us a standardized effect size of 0.5. This is the true effect size, something we would rarely know in the real world (the true effect size is unknown, we can only attempt to estimate it).
In this simulation, the studies can be categorized by nine different sample sizes, meaning they have varying true power (something we know because it’s a simulation). True power ranges all the way from 10% to 90% and each of the nine scenarios has samples simulated from a normal distribution.
.The graph above has some random variation added between points to make them out, but in reality, this (below) is what the graph looks like without any random variation at all. (These are not lines, but actual points plotted!)
The transitions can also be seen here:
Notice that despite true power being known for each of these studies, observed power highly varies within these scenarios, especially for studies with low(er) power. For example, when true power is set at 10%, many studies yield results showing “observed power” of 50%. Therefore, if we were to follow the recommendations put forth by Bababekov et al. in several scenarios, we would mistakenly put more confidence in results that truly have low power and which yield noisy estimates. Meaning it is not reliable in “improving the communication of results”.
This is because Babakev et al. does not seem to understand long-term frequencies. Statistical power is a frequentist concept, meaning that if someone designs a study with the hope of the test correctly detecting a dimensional violation by the test hypothesis (such as the null hypothesis) 80% of the time, this will occur in the long term if there is a violation of assumptions and given other assumptions.
This does not mean that the study itself has an 80% probability of correctly detecting a violation. For example, when we say that a fair coin has a 50% probability of getting either heads or tails, it does not mean we expect the coin to always give us results that fairly balance the distribution of heads and tails. We will not always expect alternating results of heads and tails (H T H T H T). In fact, it is very plausible that if we flip the coin 10 times, we may get all heads or all tails. However, in the long term, we expect the proportion of heads and tails to be fairly equal.
Furthermore, because the P-value is a random variable and measures random error in the estimate (Greenland, 2019), taking it (observed P) from a single study and transforming it into a distorted version of power (observed power) is beyond fallacious. The authors not only confuse observed power and true power, but they also confuse the random variable P with its realization, observed P. Observed P-values are useful because they indicate statistical compatibility between the observed data and the test hypothesis.
If they are being used for decision rules with a set alpha, and the researchers suspect that a type-II error was very likely, they can use the computed confidence/compatibility/consonance intervals to see what effect sizes are within the interval and how wide the interval estimates are (which measure random error/precision).
However, Bababekov et al. does not see this as a solution as they argue here,
“An alternative solution to mitigate risk of misinterpreting P > 0.05 is for surgical investigators to report the confidence intervals in their results along with the P value.”
“However, the general audience would likely pay more attention to the overlap of confidence intervals in a comparative study with two or more comparison groups with multiple confidence intervals, and still misinterpret the findings as demonstrating equivalency.”
The problem here is that investigators confusing overlapping intervals for equivalency is a cognitive problem (Greenland, 2017) where they do not understand what frequentist intervals are rather than a defect in the method itself.
A computed frequentist interval, such as a 95% confidence/consonance interval contains all effect sizes that yield P-values greater than 0.05 (Cox, 2006). Of course, the computed point estimate, often the maximum likelihood estimate (MLE), has the largest P-value, and values close to it, which will have slightly smaller P-values than the MLE, indicate greater statistical compatibility than effect sizes that are further from the MLE, which will have much smaller P-values.
Thus, it is largely irrelevant whether two or more confidence/consonance intervals overlap. The useful questions are:
Better than computing a single interval estimate for a particular alpha level is to compute the function, where every interval estimate is plotted with its corresponding alpha (10%, 15%, 25%, 50%, 90%, 95%, 99% confidence/consonance intervals), since the the 95% interval is largely arbitrary and a relic of NHST with a 5% alpha.
Bababekov et al. instead sees observed power as being a solution to the “problems” they highlight with interval estimates,
“Power provides a single metric to help readers better appreciate the limitation of a study. As such, we believe reporting power is the most reasonable solution to avoid misinterpreting P > 0.05.”
This argument further highlights the problems with trying to come to conclusions from single studies. The authors wish to answer
“Was my study large enough and reliable, and if not, what single metric can I use to better understand how reliable the decision (reject/fail to reject) is?”
For this, they have found a method, one that they reify, that helps to address their uncertainties of the data-generation process, but unfortunately, it is unreliable and cannot do what they wish it does.
As others have pointed out above, the arguments put forth in this paper are fallacious and thus the manuscript itself is defective and has the potential to seriously mislead many surgical investigators who are not well versed in statistical methods. Letters to the editor (of which there are numerous) and corrections are simply not enough. A retraction is necessary when a manuscript is this defective."
edits: some formatting and added link to the original publication
second update: included two visualizations, one with random variation between points to make out the points and not confuse them for lines, and one without any jitter
third update: added a gif to show transitions
Wow this is fantastic @zad! My only suggestion is to note that power can’t be observed. So I would put observed in quotes everywhere and explain that power depends on unobservables (both a test statistic yet to be observed and an effect size that is a hypothetical).
This reminds me of an excellent quote (I wish I remember from whom) to the effect that we need the let surgeons know that we want to learn how to do complex surgery in our spare time as biostatisticians.
Senn said this on twitter recently but didn’t attribute it to anyone…
Frank, I recall that one of your co-panelists at an JSM panel a few years back told this story. He got a call from a neurosurgeon who explained, “I’m doing a trial, but I don’t need your help; I’ll do my own stats. Can you suggest a good stats book?”
The statistician said, “I’m so glad you called! I’ve always wanted to do brain surgery; can you suggest a good book on that?”
i feel like something similar is happening with the fragility index. There is some analogy in evolution: we’re headed in a certain direction, we’re stuck the the p-value/hopthesis testing and we just build on top of it. Was it Gould’s panda’s thumb, or dawkins landscape of peaks and valleys, there’s an anology somewhere
There must be a way of converting these disputes into a betting game, letting the surgeons set the odds, and taking the opposite side. I’d have to think about this a bit more to come up with an appealing gamble for them, but clearly negative expected value.
Their informal mental model seems to be one that it can be easily “Dutch Booked” in that they will take the same data and draw different conclusions based upon an irrelevant alternative (ie. post hoc power).
I think a lot of fun can be had making this a bit more public. Economist Bryan Caplan (George Mason University) currently has an undefeated 17-0 track record when making other academics back up their prognostications with actual money.
On the observability of power: are my analogies correct?
Analogy one: the telescope.
“Using a sample to estimate both the population effect and (observed) power, is like taking a picture of the sky and using that to estimate both the average brightness of the stars and the sensitivity of the telescope. This is not possible. Or you use an instrument of known sensitivity and you estimate the population effect, or you calibate the instrument using a known population”
Analogy two: the fuel gauge.
“You cannot look at the fuel gauge and estimate from that both how many liters of fuel you have left and the sensitivity of the gauge. Either you take a calibrated gauge and you estimate how much fuel is in the tank, or you use a known amount of fuel to calibate the gauge”
As far as I know frequentism cannot answer the question “how likely is hypothesis X given the data”. Or am I misreading you?
Please help me understand this! What different conclusions about the parameter would you draw if the intervals are wide versus narrow?
Edit: a compatibility interval is (usually) just a standard error times some number, right?
