Everything I know about this issue comes from reading Dr. Stephen Senn, Dr. Harrell, or Dr. Sander Greenland. As far as I can tell, there is more agreement than disagreement among them, but I understand this might not be so obvious unless you go through a number of papers. It certainly wasn’t clear to me upon first reading a few of these.
Here are some papers (in my opinion) critical to understanding the points raised by Senn and Frank:
Lee, Y; Nelder, F (2004) Conditional and Marginal Models: Another View. Stat. Sci. 19(2) (link)
Blockquote
There has existed controversy about the use of marginal and conditional models, particularly in the analysis of data from longitudinal studies. We show that alleged differences in the behavior of parameters in so-called marginal and conditional models are based on a failure to compare like with like. In particular, these seemingly apparent differences are meaningless because they are mainly caused by preimposed unidentifiable constraints on the random effects in models. We discuss the advantages of conditional models over marginal models. We regard the conditional model as fundamental, from which marginal predictions can be made
Blockquote
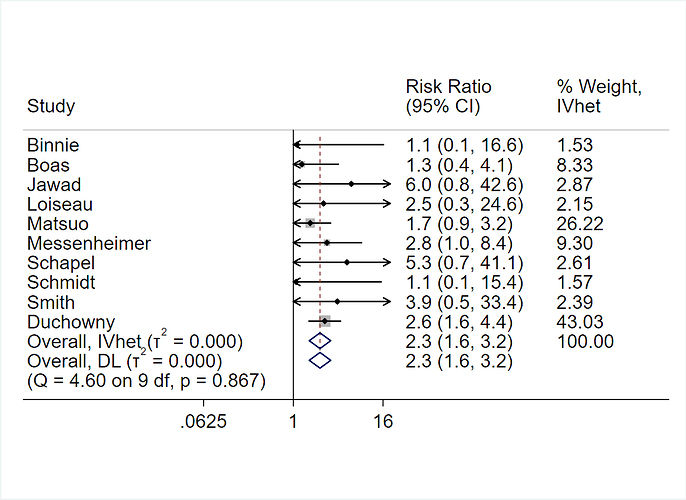
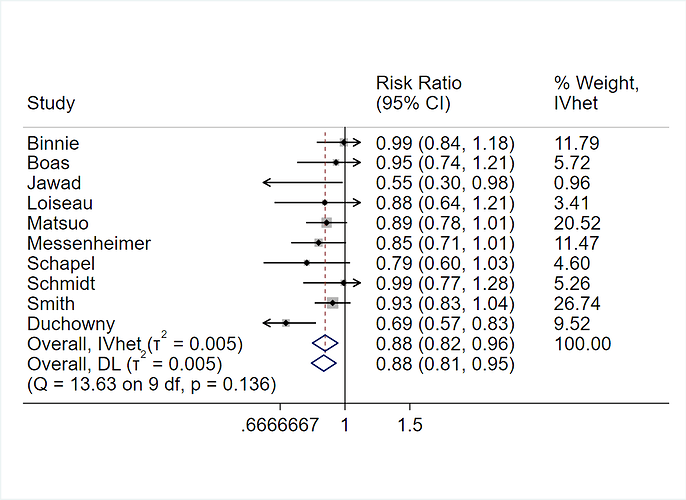
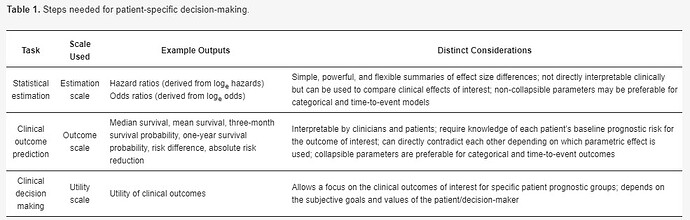
When making patient decisions, one can easily (in most situations) convert the relative effect from the first step into an absolute risk reduction if one has an estimate of the current patient’s absolute risk. This estimate may come from the same trial that produced the relative efficacy estimate, if the RCT enrolled a sufficient variety of subjects. Or it can come from a purely observational study if that study contains a large number of subjects given usual care or some other appropriate reference set.
Sander Greenland (2004), Model-based Estimation of Relative Risks and Other Epidemiologic Measures in Studies of Common Outcomes and in Case-Control Studies, American Journal of Epidemiology, Volume 160, Issue 4, 15. Pages 301–305, https://doi.org/10.1093/aje/kwh221
Blockquote
Some recent articles have discussed biased methods for estimating risk ratios from adjusted odds ratios when the outcome is common, and the problem of setting confidence limits for risk ratios. These articles have overlooked the extensive literature on valid estimation of risks, risk ratios, and risk differences from logistic and other models, including methods that remain valid when the outcome is common, and methods for risk and rate estimation from case-control studies. The present article describes how most of these methods can be subsumed under a general formulation that also encompasses traditional standardization methods and methods for projecting the impact of partially successful interventions. Approximate variance formulas for the resulting estimates allow interval estimation; these intervals can be closely approximated by rapid simulation procedures that require only standard software functions.
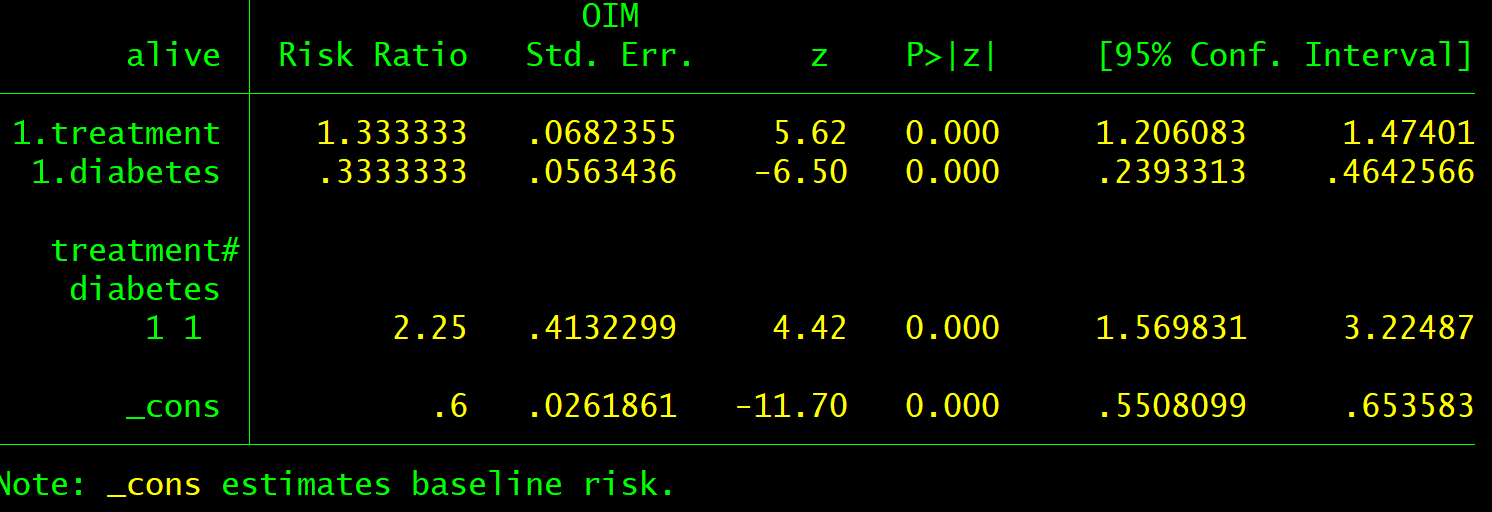
Both epidemiologists and scientists performing clinical trials can use logistic regression to develop models to help clinicians and patients select the most relevant treatments. Do the statistics on the (additive) log odds scale, but convert baseline risks to the probability scale.
Someone please correct me if I’m mistaken here.