I have gone over the paper again carefully. The assumption on which the whole paper is based is ‘consistency’. To quote from the paper: “At the individual level, the connection between behaviors in the two studies relies on an assumption known as ‘consistency’ (Pearl, 2009, 2010), asserting that an individual response to treatment depends entirely on biological factors, unaffected by the settings in which treatment is taken. In other words, the outcome of a person choosing the drug would be the same had this person been assigned to the treatment group in an RCT study. Similarly, if we observe someone avoiding the drug, their outcome is the same as if they were in the control group of our RCT. In terms of our notation, consistency implies: P(yt|t) = P(y|t), P(yc|c) = P(y|c).”
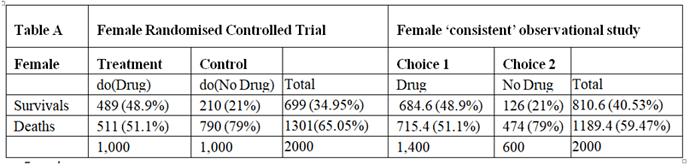
However, according to their example data for females:
P(yt|t) = 489/1000 = 0.489, P(y|t)= 378/1000 =0.378, P(yc|c) = 210/1000=0.210, P(y|c)=420/600 = 0.7
So that P(yt|t) ≠ P(y|t), P(yc|c) ≠ P(y|c)
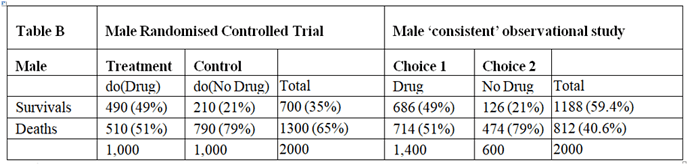
According to their example data for males:
P(yt|t) = 49/1000 = 0.49, P(y|t)= 980/1400 = 0.7, P(yc|c) = 210/100=0.210, P(y|c)=420/600=0.7
So that P(yt|t) ≠ P(y|t), P(yc|c) ≠ P(y|c)
This means that the assumption of consistency is not applicable to the paper’s example data of their RCT and observational study. However, they go on to make the calculations nevertheless “based on this assumption (i.e. of ‘consistency’), and leveraging both experimental and observational data, Tian and Pearl (Tian and Pearl, 2000) derived the following tight bounds on the probability of benefit, as defined in equation (3): P(benefit) = P(yt, y′c). Therefore the estimated probability bounds in their inequality equation (5) do not follow from their assumptions and reasoning. However, by applying these probability bounds they arrive at point estimates of the probability of counterfactual ‘benefit’ and ‘harm’ (the latter are defined in my previous post (Individual response - #205 by HuwLlewelyn).
I created new example data for males and females where the RCT data were identical and the proportions choosing to take the drug and not to take it were the same as in their observational example. However in my new observational study data, P(yt|t) = P(y|t) and P(yc|c) = P(y|c) so that the assumption of ‘consistency’ could be applied. I then applied their calculations to this data that I had created.
Instead of getting point estimates I got probability ranges. For females the probability of ‘benefit’ counterfactually (e.g. by giving treatment, turning the clock back and giving placebo) was between 0.279 and 0.489 and the probability of ‘harm’ was between 0 and 0.21. For males the probability of ‘benefit’ was between 0.28 and 0.49 and the probability of ‘harm’ was between 0 and 0.21. (p(Harm) = p(Benefit) – CATE, which was 0.279 and 0.28 for females and males respectively). The calculations are in the Appendix below. If the assumption of consistency is valid, we can tell all this from the RCT alone: p(Benefit) ≥ Pr(yt) - Pr(yc) and P(Benefit) ≤ Pr(yt) and p(Harm) = p(Benefit) - (Pr(yt) - Pr(yc)), so that the observational study adds nothing in this context. As we have discussed already, observational studies can be useful in other ways such as detecting adverse effects.
Appendix
Female RCT and ‘consistent’ observational study
Calculations for females (replacing those on pages 8 and 9 in the paper), when Pr indicates that the probability is from the RCT and Po indicates that the probability is derived form the observation study:
P(Benefit) ≥ 0
P(Benefit) ≥ Pr(yt) - Pr(yc) = 489/1000 -210/1000 = 279/1000 = CATE = 0.279
P(Benefit) ≥ Po(y) - Pr(yc) = 0.4053 – 0.21 = 0.1953
P(Benefit) ≥ Pr(yt) - Po(y) = 0.489-0.4053 = 0.0807
P(Benefit) ≤ Pr(yt) = 489/1000 = 0.489
P(Benefit) ≤ Pr(y’c) = 790/1000 = 0.79
P(Benefit) ≤ Po(t, y) + Po(c, y’) = 686/2000 + 474/2000 = 0.343 +0.237 = 0.58
P(Benefit) ≤ Pr(yt) − Pr(yc) + Po(t, y′) + Po(c, y) = 0.489-0.21 +0.357+0.063 = 0.6997
Therefore:
0.279 ≤ p(Benefit) ≤ 0.489 and (0.279-0.279) = 0 ≤ p(Harm) ≤ 0.21 = (0.489-0.279)
Male RCT and ‘consistent’ observational study
Calculations for Males (replacing those on pages 8 and 9 in the paper):
P(Benefit) ≥ 0
P(Benefit) ≥ Pr(yt) - Pr(yc) = 490/1000 -210/1000 = 280/1000 = 0.28 = CATE = 0.28
P(Benefit) ≥ Po(y) - Pr(yc) = 0.406 – 0.21 = 0.196
P(Benefit) ≥ Pr(yt) - Po(y) = 0.49-0.406 = 0.084
P(Benefit) ≤ Pr(yt) = 49/1000 = 0.49
P(Benefit) ≤ Pr(y’c) = 790/1000 = 0.79
P(Benefit) ≤ Po(t, y) + Po(c, y’) = 686/2000 + 474/2000 = 0.343+0.237 = 0.58
P(Benefit) ≤ Pr(yt) − Pr(yc) + Po(t, y′) + Po(c, y) = 0.49-0.21 +0.357+0.63 = 0.7
Therefore:
0.28 ≤ p(Benefit) ≤ 0.49 and (0.28-0.28) = 0 ≤ p(Harm) ≤ 0.21 = (0.49-0.28)